Tidytuesday 2020-06-02: Marbula One race simulation
Introducción

El #tidytuesday del 2020-06-02 pone a nuestra disposición un conjunto de datos de las carreras de canicas de la Marbula One: ocho carreras (con sus correspondientes tandas clasificatorias) con sus participantes y los tiempos de llegada.
La animación simula la última tanda clasificatoria (S1Q8) del campeonato de canicas Marbula One. Decimos que se trata de una simulación, ya que:
- En las tandas clasificatorias las canicas salen de una en una (y no todas a la vez, como en la animación).
- No disponemos de los tiempos parciales de cada canica, solo el tiempo total. Vamos a extrapolar tiempos de paso para canica teniendo en cuanta únicamente el tiempo final, por lo que no vamos a poder tiempos y puntos de paso exactos (por lo que si, por ejemplo, ha habido adelantamientos, no se reflejarán en la animación).
Esta animación consta de dos componentes principales:
- El circuito de carreras
- La carrera de canicas propiamente dicha.
Cargar librerías y fuentes
Antes de empezar a trabajar, cargamos las librerías y las fuentes con las que vamos a trabajar.
library(here)
library(tidyverse)
library(ggforce)
library(ggtext)
library(gganimate)
library(extrafont)
library(showtext)
loadfonts(device = "win", quiet = TRUE)
font_add_google(name = "Racing Sans One", family = "Racing Sans One")
showtext_auto()Gráfico estático de base: circuito Midnight Bay.
El conjunto de datos original no contiene ninguna información sobre los circuitos, por lo que para poder recrear el circuito de la octava carrera he transportado el circuito que se ve en el vídeo de la competición (a partir del segundo 53) a mi propio sistema de coordenadas x/y.
Podríamos dibujar el circuito con los geoms de ggplot geom_segment() y geom_curve, pero vamos a usar los geoms de la extensión para ggplot ggforce, ya que nos ofrecen una ventaja muy importante de cara a calcular las coordenadas de paso de las canicas: con el argumento n podemos indicar cuántos puntos queremos calcular dentro del segmento en cuestión, lo que resulta especialmente útil en el caso de las curvas.
Para ello, he dividido el circuito en tramos de distancia similar, de unas dos unidades de longitud. En el caso de las curvas, hemos calculado los puntos para arcos de 90 grados, aunque podríamos darle a cualquiera su propio ángulo.
La razón para hacerlo de esta forma consiste en que cuando calculemos puntos intermedios siempre calcularemos el mismo número, independientemente de la longitud del arco; si tuvieran longitudes distintas, un arco de 90º tendría una red de puntos intermedios más tupida que la de un arco de 180º u otro de 270º, lo que acabaría afectando a la fluidez de la animación (las canicas parecerían ralentizarse en las curvas cortas, mientras que se acelerarían en las largas).
Con características en mente, he preparado el siguiente boceto del circuito:

Con el boceto como base, he creado un conjunto de datos circuito.csv que recoge las siguientes variables:
- Sector: tal y como se indica en el vídeo
- Tramo: los tramos que hemos diseñado en el boceto, importante para poder ordenar la animación correctamente
- Tipo:
recta|curvapara el circuito propiamente dicho;rectanguloolabelpara otros elementos (nombres de las curvas, etc.) - Color y fill: los geoms de tipo línea no aceptan estos dos
aesthetics(solocolor), por lo que duplicaremos las marcas gráficas: una capa inferior con una anchura mayor y usando el valor de la variablecolor, y una capa superior de anchura menor y que usará la variablefill; de esta forma conseguiremos el efecto deseado. - x, y, xend e yend: coordenadas x/y de los puntos de inicio y final de las rectas
- x0, y0: punto central de los arcos
- r: radio de los arcos
- start y end: ángulo de inicio y final de los arcos (se tienen que dar en radianes, los terminaremos de calcular más adelante; de momento solo se recogen los valores 0.5, 1, 1.5 y 0/2 -dependiendo de la dirección del arco)
- xmin, xmax, ymin e ymax: para dibujar los rectángulos.
circuito <- read_csv(here("static","data","circuito.csv"))
head(circuito)## # A tibble: 6 x 18
## sector tramo tipo color fill x y xend yend x0 y0 r start
## <chr> <chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Secto~ 1 recta deep~ black 16 11 16 13 NA NA NA NA
## 2 Secto~ 2 recta deep~ white 16 13 16 15 NA NA NA NA
## 3 Secto~ 3 curva deep~ white NA NA NA NA 18 15 2 1.50
## 4 Secto~ 4 curva deep~ white NA NA NA NA 18 15 2 0
## 5 Secto~ 5 recta deep~ white 20 15 20 13 NA NA NA NA
## 6 Secto~ 6 recta deep~ white 20 13 20 11 NA NA NA NA
## # ... with 5 more variables: end <dbl>, xmin <dbl>, ymin <dbl>, xmax <dbl>,
## # ymax <dbl>Dibujar el circuito capa por capa
Aunque no es necesario fragmentar el código, lo muestro de esta forma para entender mejor la forma en la que se construye el circuito.
Rectángulos
( p <- ggplot() +
# capa con rectángulos grises
geom_rect(
data = circuito %>% filter(tipo == "rectangulo"),
aes(
xmin = xmin,
ymin = ymin,
xmax = xmax,
ymax = ymax,
fill = fill
)
)
)
Rectas en capa inferior
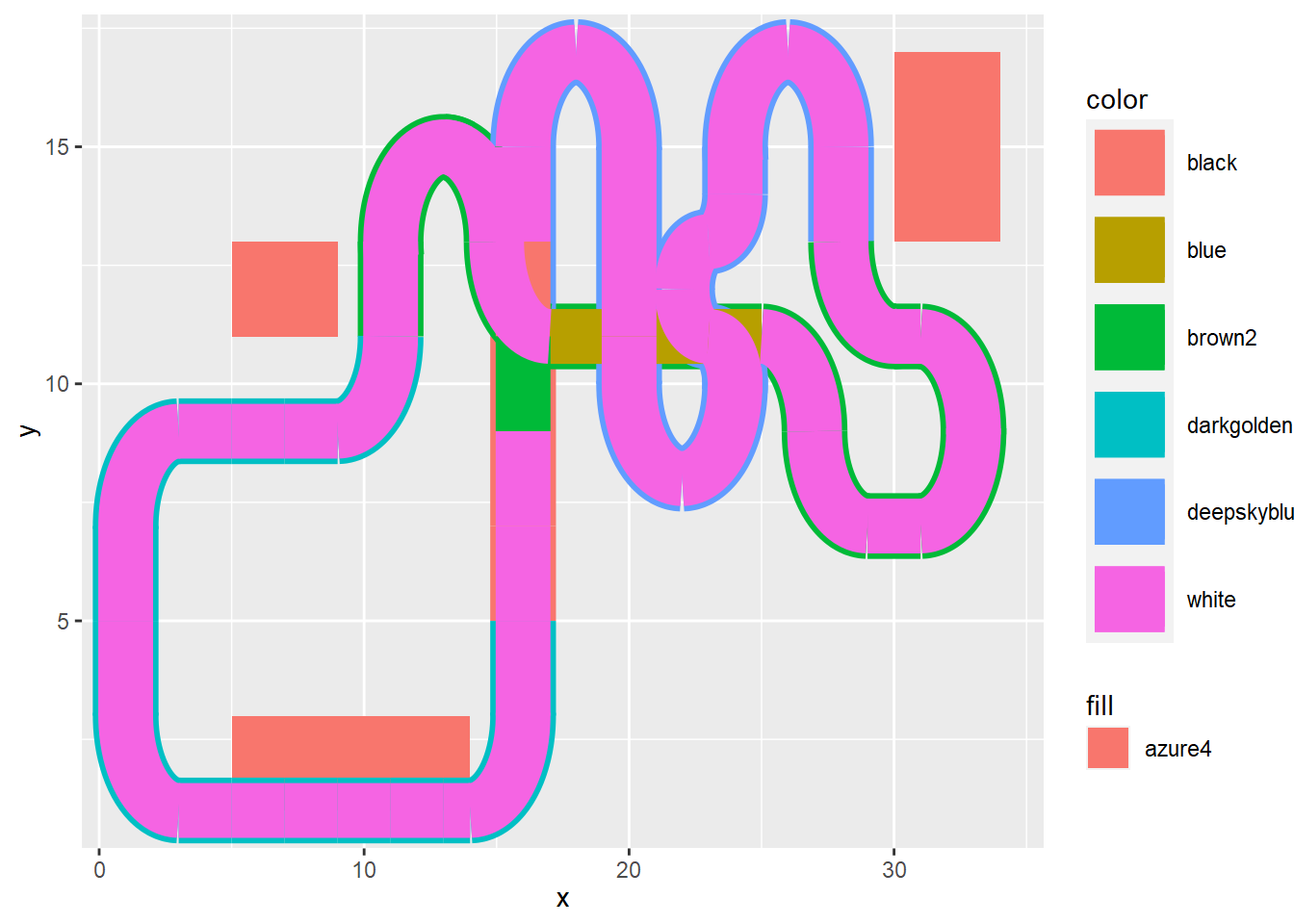
# capa inferior con rectas de color
( p <- p + geom_link(
data = circuito %>% filter(tipo == "recta"),
aes(
x = x,
y = y,
xend = xend,
yend = yend,
color = color
),
size = 12,
n = 45
)
) 
Curvas en capa inferior
# capa inferior con curvas de color
( p <- p + geom_arc(
data = circuito %>% filter(tipo == "curva"),
aes(
x0 = x0,
y0 = y0,
r = r,
start = start * pi,
end = end * pi,
color = color
),
size = 12,
n = 90
)
)
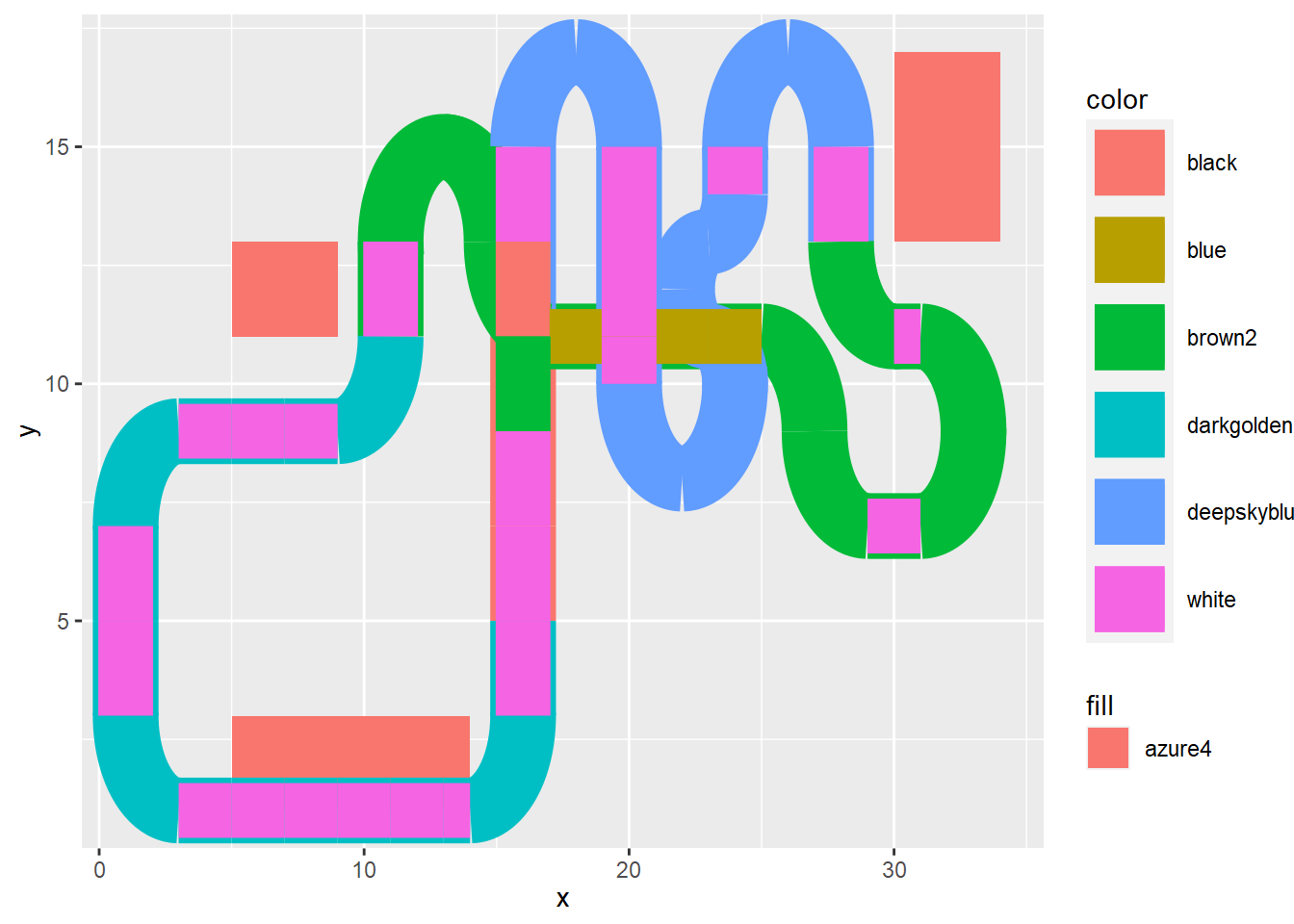
Rectas en capa superior
Para crear el efecto visual de que las líneas tienen dos colores superpondremos dos capas con los mismos datos, salvo el grosor y el color de la línea.
# capa superior con rectas blancas
( p <- p + geom_link(
data = circuito %>% filter(tipo == "recta"),
aes(
x = x,
y = y,
xend = xend,
yend = yend,
color = fill
),
size = 10,
n = 45
)
)
Curvas en capa superior
# capa superior con curvas blancas
( p <- p + geom_arc(
data = circuito %>% filter(tipo == "curva"),
aes(
x0 = x0,
y0 = y0,
r = r,
start = start * pi,
end = end * pi,
color = fill
),
size = 10,
n = 90
)
)
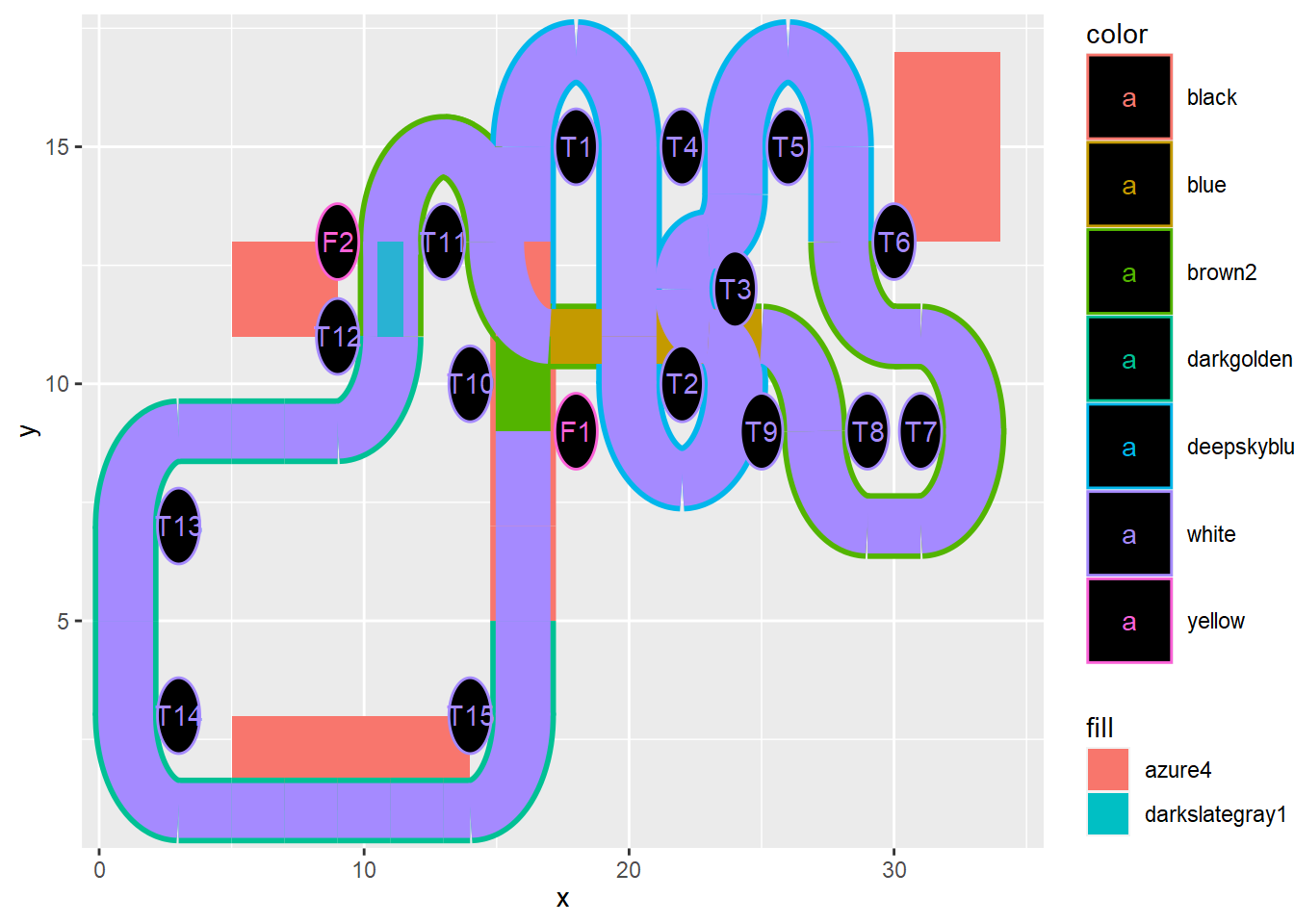
Resto de elementos
# rectángulo azul que simula tramo acristalado
( p <- p + geom_rect(
data = circuito %>% filter(tipo == "rectangulo_sup"),
aes(
xmin = xmin,
ymin = ymin,
xmax = xmax,
ymax = ymax,
fill = fill
),
alpha = 0.75
) +
# círculos para los códigos de las curvas
geom_circle(
data = circuito %>% filter(tipo == "label"),
aes(
x0 = x0,
y0 = y0,
r = r,
color = color
),
fill = "black"
) +
# textos con los códigos de las curvas
geom_text(
data = circuito %>% filter(tipo == "label"),
aes(
x = x,
y = y,
label = tramo,
color = color
)
)
)
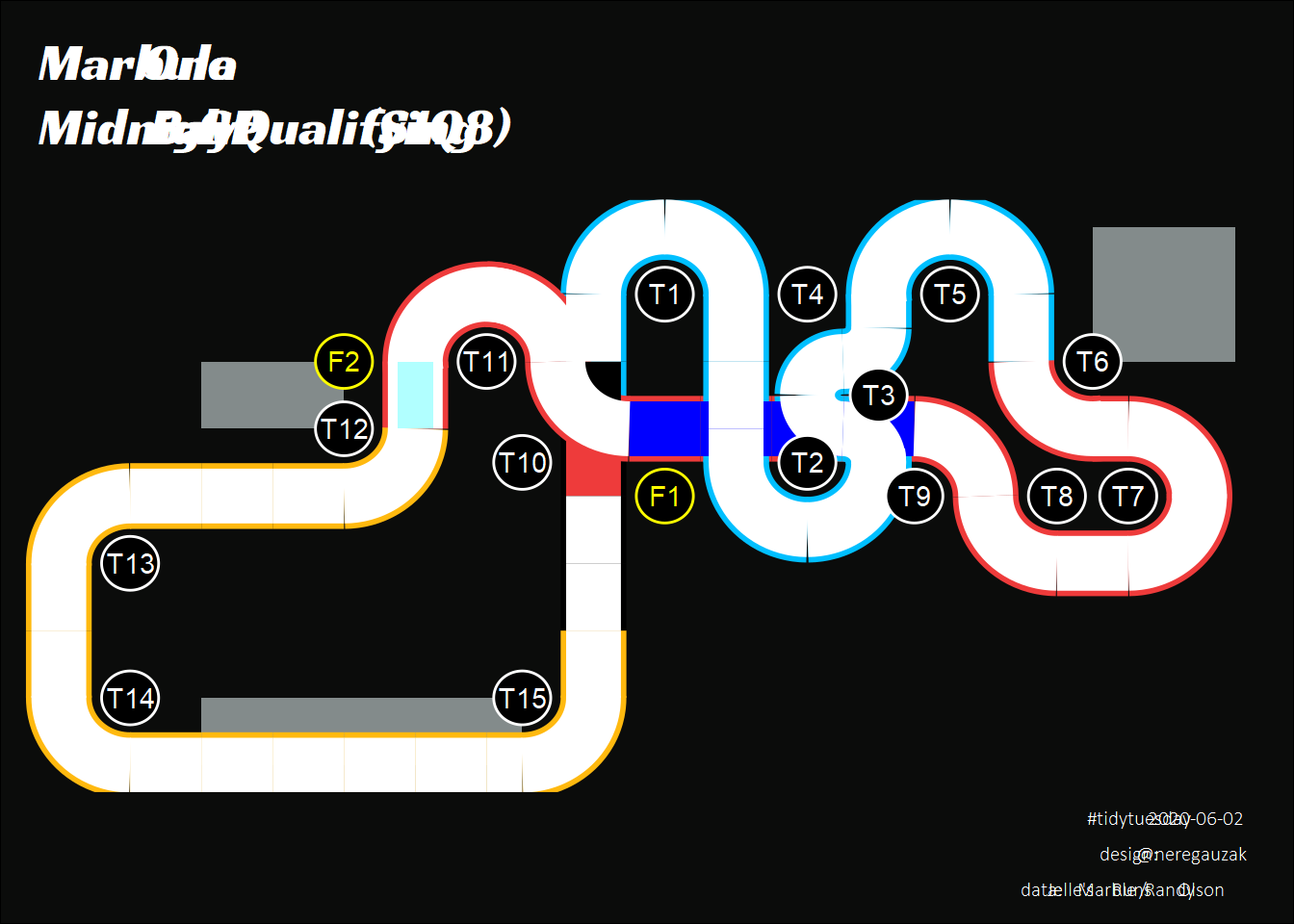
Finalmente, realizamos algunas modificaciones en el tema gráfico. Dado que los colores están ya codificados en el conjunto de datos, usamos escalas de tipo identity para color y fill.
# los colores están almacenados como nombres de color aceptados por R,
# por lo que usamos scale identity
( p <- p +
scale_colour_identity() +
scale_fill_identity() +
labs(title = "<span style='size: 1.25em'>Marbula One</span><br />
Midnight Bay GP Qualifying (S1Q8)",
caption = "#tidytuesday 2020-06-02<br />
design: @neregauzak<br />
data: Jelle's Marble Runs / Randy Olson") +
theme_void() +
theme(
plot.title = element_markdown(
family = "Racing Sans One",
color = "white",
size = 20,
lineheight = 1.25,
margin = margin(
t = 25,
r = 15,
b = 20,
l = 15
)
),
plot.caption = element_markdown(
family = "Calibri Light",
color = "white",
size = 8,
lineheight = 1.75,
hjust = 0.95,
margin = margin(
t = 10,
r = 15,
b = 10,
l = 15
)
),
plot.background = element_rect(fill = rgb(0.043, 0.047, 0.043))
)
)
Calcular las coordenadas de cada tramo del circuito
A fin de crear una animación más fina, vamos a crear un circuito con más tramos de los que teníamos en el dataset original. Esto es posible gracias a los geoms de ggforce, que como ya hemos mencionado permiten crear secciones de los tramos que ya hemos creado.
Inicialmente hemos indicado que se crearan 45 segmentos para cada tramo de recta y 90 para cada tramo de curva, pero no vamos a necesitar tantos puntos, por lo que vamos a quedarnos con cuatro puntos por cada tramo.
Obtener datos de ggplot
Podemos extraer los datos calculados por ggplot y sus extensiones con varias funciones. La más genérica es ggplot_build(), que devuelve una estructura de datos compleja, formada por varias listas y sublistas (dependiendo de las capas que hayamos usado). Si, por ejemplo, quisieramos acceder a los datos de la segunda capa (la capa inferior de rectas) podríamos almacenar los datos de ggplot en un objeto con datos_ggplot <- ggplot_build(p) y posteriormente extraer los datos de dicha capa con datos_ggplot$data[[2]].
Como solo necesitamos los datos de dos capas, podemos usar la función layer_data() para extraer directamente los datos de la capa de interés.
# almacenamos los datos calculados por ggplot/ggforce
plot_data_rectas <- layer_data(p, i = 2)
plot_data_curvas <- layer_data(p, i = 3)Vamos a echar un vistazo al aspecto que tienen los datos que hemos recuperado de ggplot:
head(plot_data_rectas, 10)## colour PANEL x y index group size linetype alpha
## 1 deepskyblue1 1 16 11.00000 0.00000000 4 12 1 NA
## 2 deepskyblue1 1 16 11.04545 0.02272727 4 12 1 NA
## 3 deepskyblue1 1 16 11.09091 0.04545455 4 12 1 NA
## 4 deepskyblue1 1 16 11.13636 0.06818182 4 12 1 NA
## 5 deepskyblue1 1 16 11.18182 0.09090909 4 12 1 NA
## 6 deepskyblue1 1 16 11.22727 0.11363636 4 12 1 NA
## 7 deepskyblue1 1 16 11.27273 0.13636364 4 12 1 NA
## 8 deepskyblue1 1 16 11.31818 0.15909091 4 12 1 NA
## 9 deepskyblue1 1 16 11.36364 0.18181818 4 12 1 NA
## 10 deepskyblue1 1 16 11.40909 0.20454545 4 12 1 NAhead(plot_data_curvas, 10)## colour group index PANEL nControl x y size linetype
## 1 deepskyblue1 3 0.00000000 1 23 16.00000 14.99937 12 1
## 2 deepskyblue1 3 0.04545455 1 23 16.00505 15.14208 12 1
## 3 deepskyblue1 3 0.09090909 1 23 16.02028 15.28406 12 1
## 4 deepskyblue1 3 0.13636364 1 23 16.04559 15.42460 12 1
## 5 deepskyblue1 3 0.18181818 1 23 16.08087 15.56297 12 1
## 6 deepskyblue1 3 0.22727273 1 23 16.12593 15.69847 12 1
## 7 deepskyblue1 3 0.27272727 1 23 16.18055 15.83041 12 1
## 8 deepskyblue1 3 0.31818182 1 23 16.24444 15.95812 12 1
## 9 deepskyblue1 3 0.36363636 1 23 16.31728 16.08095 12 1
## 10 deepskyblue1 3 0.40909091 1 23 16.39870 16.19826 12 1
## alpha lineend
## 1 1 butt
## 2 1 butt
## 3 1 butt
## 4 1 butt
## 5 1 butt
## 6 1 butt
## 7 1 butt
## 8 1 butt
## 9 1 butt
## 10 1 buttCalcular los puntos de control del circuito
Como vemos, vamos a tener que trabajar por separado, ya que la estructura de los datos no es idéntica.
Hay que hacerlo por separado para rectas y curvas, porque están almacenadas de forma distinta. En un último paso tendremos que unir y ordenar todos los datos de rectas y curvas; para poder ordenar los puntos de paso correctamente, necesitaremos una combinación de las variables tramo (del conjunto de datos original) e index (correspondiente al argumento n calculado por ggforce).
Sin embargo, como no hemos usado la variable tramo a la hora de generar el gráfico, no consta en los datos recuperados de ggplot.
He probado varios métodos para poder reincorporar este dato, pero lamentablemente al final he tenido que hacerlo manualmente; la cuestión es que ggforce genera un par de nuevas variables para los segmentos intermedios, group e index. En principio, deberíamos poder usar la variable group para poder ordenar los registros, pero parece ser que no se aplica el mismo orden que a las filas del conjunto de datos original. Es decir, a la primera fila no se le asigna el group 1 (me queda investigar en profundidad cómo funcionan los geoms de ggforce).
Por tanto, he tenido que mapear en dos tablas los grupos y tramos de rectas y curvas, para luego combinarlas con los datos de ggplot vía left_join.
# Obtenemos las posiciones x e y calculadas por ggplot
# para rectas y nos quedamos con cuatro puntos por tramo
datos_rectas_todo <- plot_data_rectas %>%
filter(index == 0 |
index == 0.25 | index == 0.5 | index == 0.75)
id_tramos_rectas <-
read_csv(
here("static", "data", "union_rectas_grupos_tramos.csv"),
col_names = TRUE,
cols(group = col_character(),
tramo = col_character())
)
datos_rectas_todo <- datos_rectas_todo %>%
left_join(id_tramos_rectas, by = "group")
# Obtenemos las posiciones x e y calculadas por ggplot
# para curvas y nos quedamos con cuatro puntos por tramo
datos_curvas_todo <- plot_data_curvas %>%
filter(index == 0 |
(index > 0.245 &
index < 0.28) | index == 0.5 | (index > 0.72 & index < 0.76))
id_tramos_curvas <-
read_csv(
here("static", "data", "union_curvas_grupos_tramos.csv"),
col_names = TRUE,
cols(group = col_character(),
tramo = col_character())
)
# combinamos los datos
datos_curvas_todo <- datos_curvas_todo %>%
left_join(id_tramos_curvas, by = "group")Ahora ya podemos combinar y ordenar correctamente el dataset por puntos de control.
# Combinamos y ordenamos puntos de rectas y curvas
datos <- bind_rows(datos_rectas_todo, datos_curvas_todo, .id = "tipo") %>%
select(tipo, tramo, index, x, y) %>%
arrange(as.numeric(tramo), index) %>%
mutate(tramo = as.numeric(tramo),
punto_control = row_number())Si recreamos el circuito con los números de tramo podremos comprobar si se han ordenado correctamente o no:
ggplot(datos, aes(x, y, color = tramo)) +
geom_text(aes(label = punto_control), size = 3)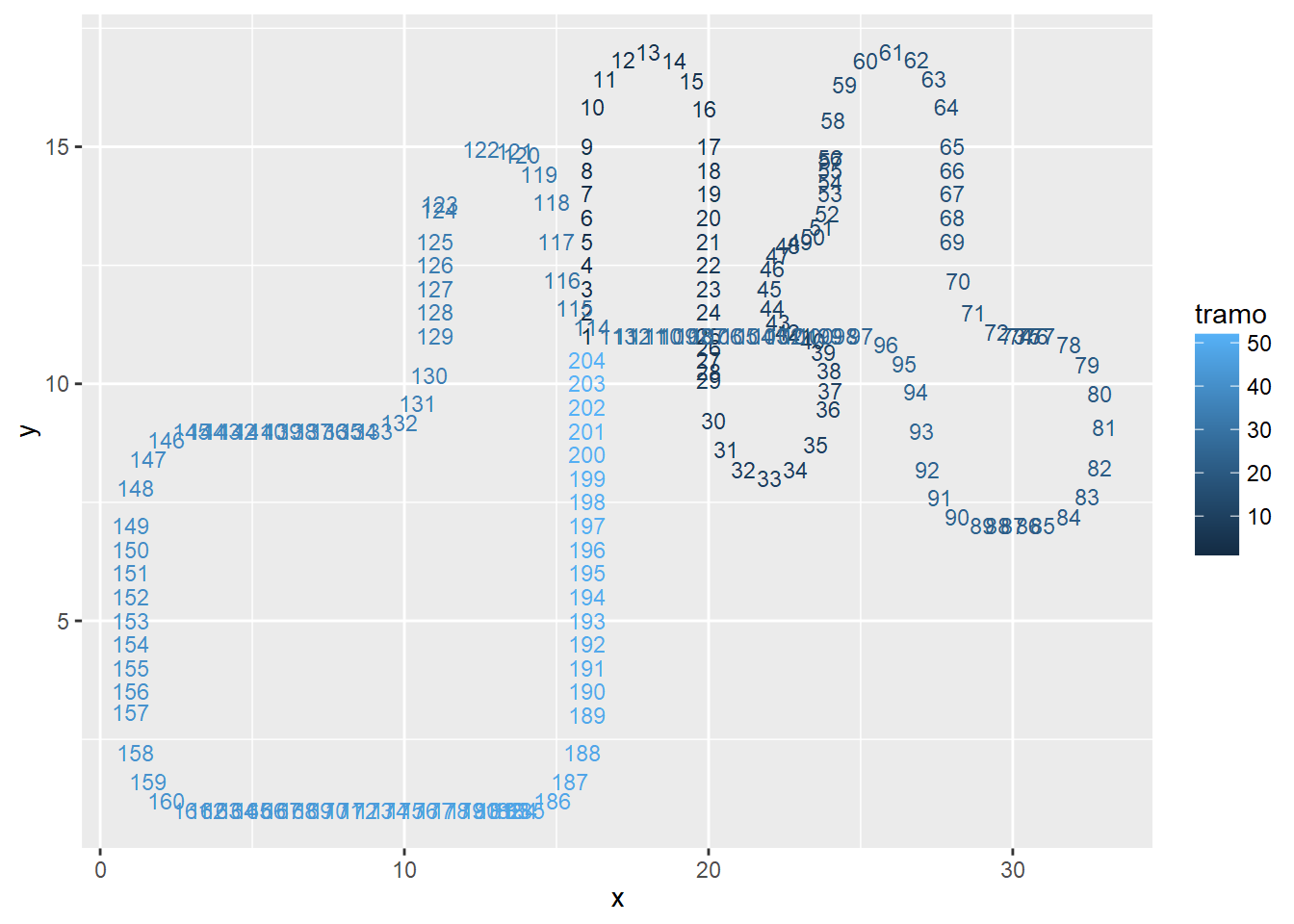
Preparar datos de las canicas
Los pasos más importantes consisten en:
- Tenemos que multiplicar los datos referentes a S1Q8 tantas veces como pasos queramos crear en la animación, considerando que a más pasos la nimación final será más fina, pero llevará más tiempo de renderizado. Usaremos como referencia para los cálculos el tiempo de la canica ganadora, que es de 24.5 segundos (se ha redondeado el tiempo).
En la animación crearemos un número de pasos múltiplo de dicha cifra, por lo que tenemos que generar la estructura de datos que almacene todos los puntos de la animación para cada canica.
Tras varias pruebas, he optado por crear una animación con 98 pasos (24,5* 4).
Antes de transformar la estructura calculamos la velocidad (en puntos de control por segundo, teniendo en cuenta que hemos creado 204 puntos de control) de cada canica. Para poder unir los datos correctamente, primero redondeamos el tiempo a cero decimales.
La función slice(), combinada con la función rep(), nos permitirá crear la estructura necesaria para tener 98 pasos para cada canica.
Una vez que tenemos la nueva estructura, computamos el número de paso y calculamos en qué punto de control está cada canica para cada paso.
marbles <- readr::read_csv('https://raw.githubusercontent.com/rfordatascience/tidytuesday/master/data/2020/2020-06-02/marbles.csv')
canicas <- marbles %>%
filter(race == "S1Q8") %>%
select(marble_name, time_s) %>%
mutate(time_s = round((round(time_s, 1) * 4), 0),
velocidad = 204 / time_s) %>%
slice(rep(row_number(), 98)) %>%
arrange(marble_name) %>%
group_by(marble_name) %>%
mutate(
paso = row_number(),
punto_control = round((velocidad * paso), 0),
color = case_when(
marble_name == "Bolt" ~ "blue",
marble_name == "Clementin" ~ "darkorange",
marble_name == "Clutter" ~ "seagreen1",
marble_name == "Hazy" ~ "azure3",
marble_name == "Hive" ~ "darkgoldenrod4",
marble_name == "Mallard" ~ "limegreen",
marble_name == "Momo" ~ "darkolivegreen3",
marble_name == "Prim" ~ "chocolate2",
marble_name == "Rezzy" ~ "deeppink1",
marble_name == "Rojo Uno" ~ "darkorange",
marble_name == "Snowy" ~ "grey90",
marble_name == "Speedy" ~ "firebrick",
marble_name == "Starry" ~ "lightsteelblue1",
marble_name == "Sublime" ~ "chartreuse2",
marble_name == "Wospy" ~ "blue4",
marble_name == "Yellup" ~ "yellow",
TRUE ~ "ivory3"
)
)Obtener coordenadas para cada paso de las canicas
Una vez que tenemos la estructura correcta, unimos las distintas tablas para traer las coordenadas correctas para cada canica y paso.
# Combinamos todos los datos
recorridos_canicas <- canicas %>%
left_join(datos, by ="punto_control")Antes de generar la animación, comprobamos que los trazados son correctos con un gráfico de líneas.
# prueba
ggplot(data = recorridos_canicas, aes(x, y, color = marble_name)) +
geom_path()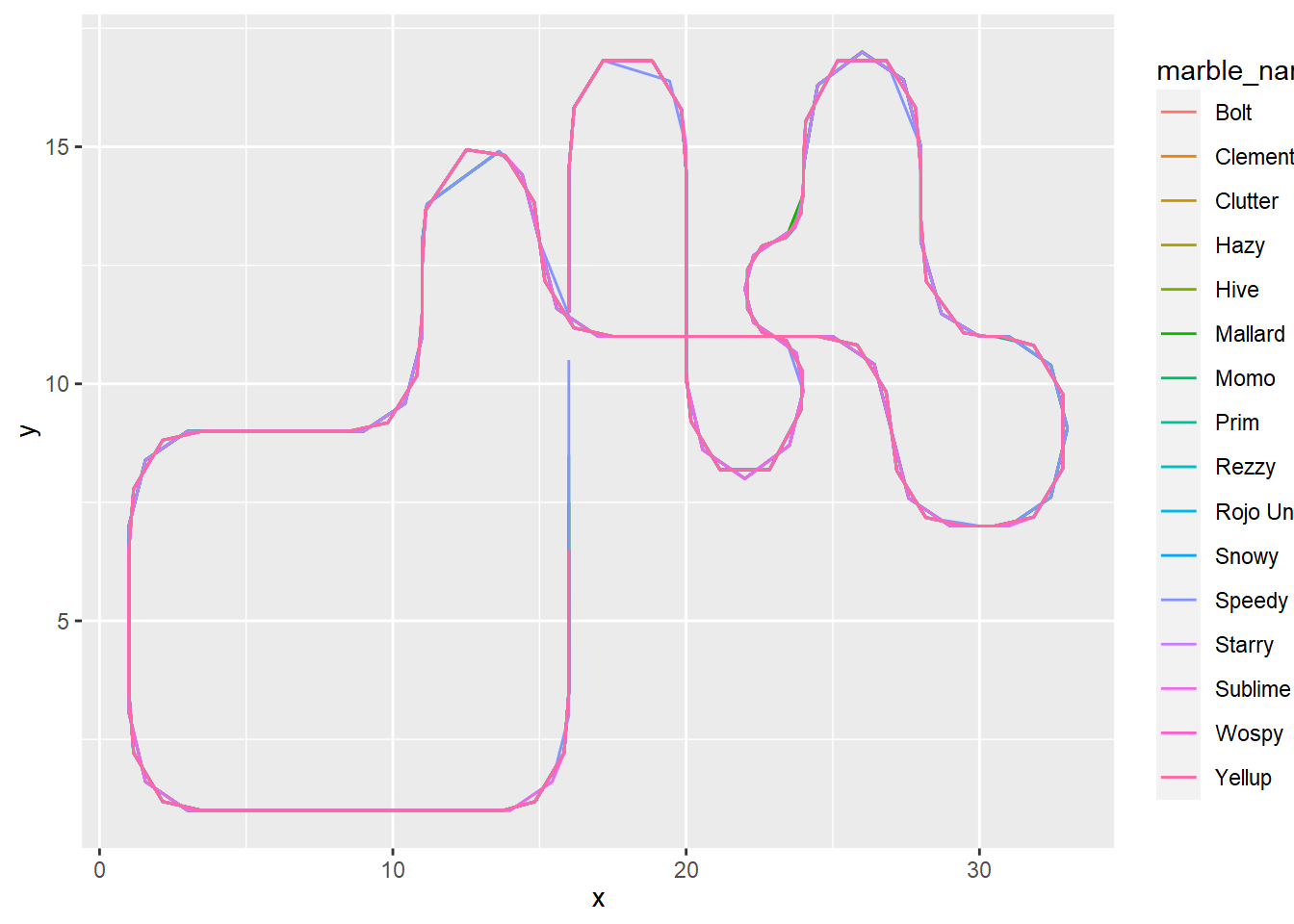
Animación
Antes de crear la animación tenemos que añadir los puntos que simularán las canicas, y que serán los elementos gráficos que se animarán.
Usamos geom_jitter() para que las marcas no se solapen entre sí.
options(gganimate.dev_args = list(res=105))
anim <- p + geom_jitter(
data = recorridos_canicas,
aes(x = x, y = y, fill = color),
shape = 21,
size = 4,
color = "black",
width = 0.2,
height = 0.2
) +
transition_states(
as.numeric(paso),
transition_length = 3,
state_length = 1,
wrap = FALSE
)
animate(anim, nframes = 392, start_pause = 10, end_pause = 20, width = 1250, height = 800)
anim_save("marbula_one_S1Q8_2.gif", animation = last_animation(), path = here("static", "images", "marbula_one_S1Q8_2.gif"))