Interacción entre variables cuantitativas, discretas y geoms geométricos básicos en ggplot2: puntos, barras y rectángulos
Herramientas: ggplot2
Introducción
Estoy preparando un curso básico para personas que no han trabajado nunca con ggplot2, y pensando en los temas que tratar me ha dado por trastear con los geoms más habituales y los distintos tipos de variables, creando todas las posibles combinaciones.
Ggplot espera unas combinaciones determinadas (por ejemplo, una variable continua para geom_histogram())… pero ¿qué pasa si forzamos la máquina y jugamos con todas las combinaciones posibles?
Lo que pasa es que en algunos casos la combinación será la correcta, en otros casos será incorrecta y ggplot nos mostrará un mensaje de error (y ningún gráfico)… y otras veces, ggplot2 creará un gráfico pero probablemente no sea lo que esperábamos y/o creíamos que iba a crear.
Como las posibles combinaciones son muchas, en este primer post trataré sobre los geoms para crear las marcas gráficas elementales, a saber, puntos (y rectángulos) y barras/columnas. En otros post trataré los gráficos de líneas y áreas.
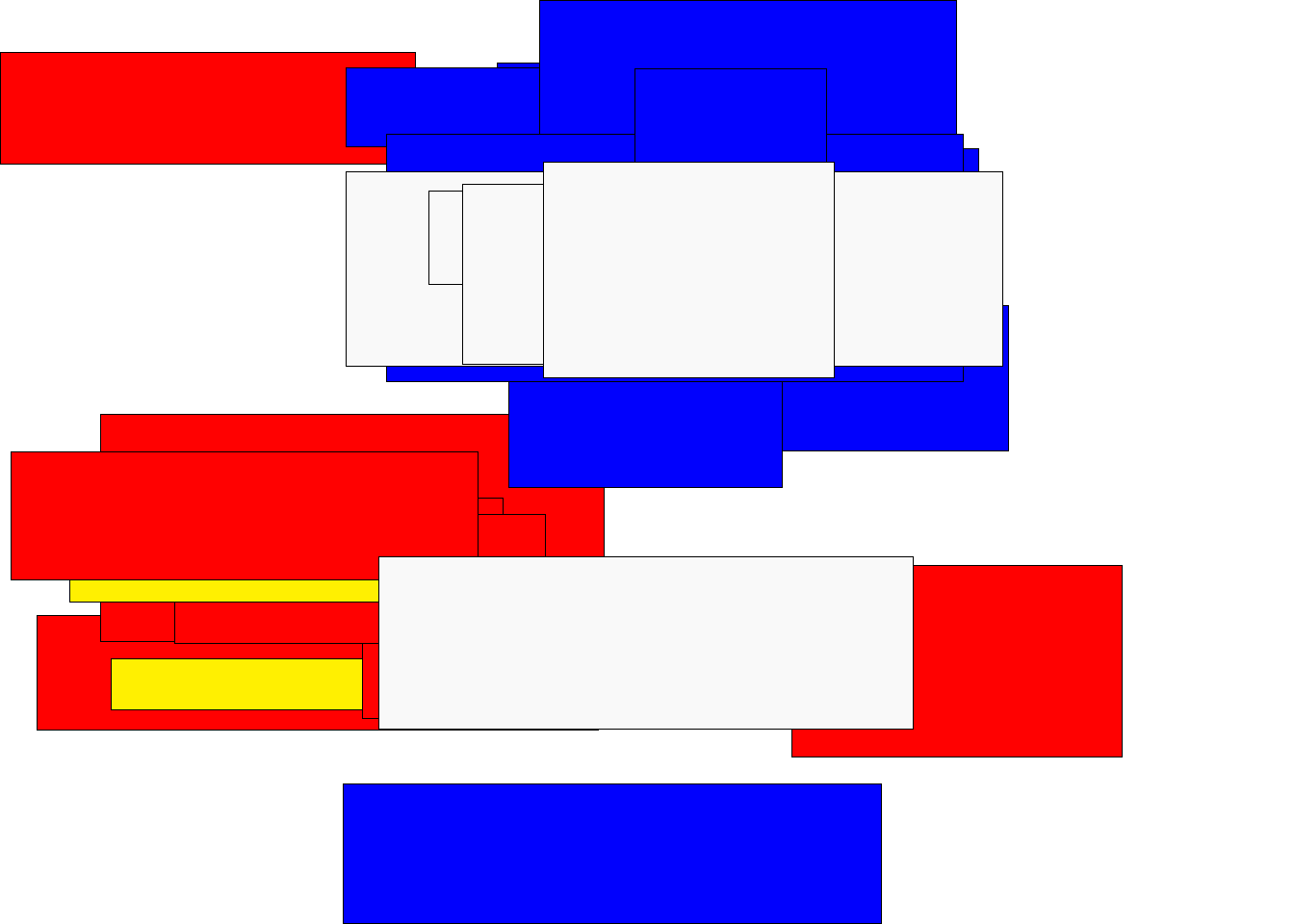
¡Al final seremos capaces de crear nuestro propio cuadro de Mondrian con ggplot2!
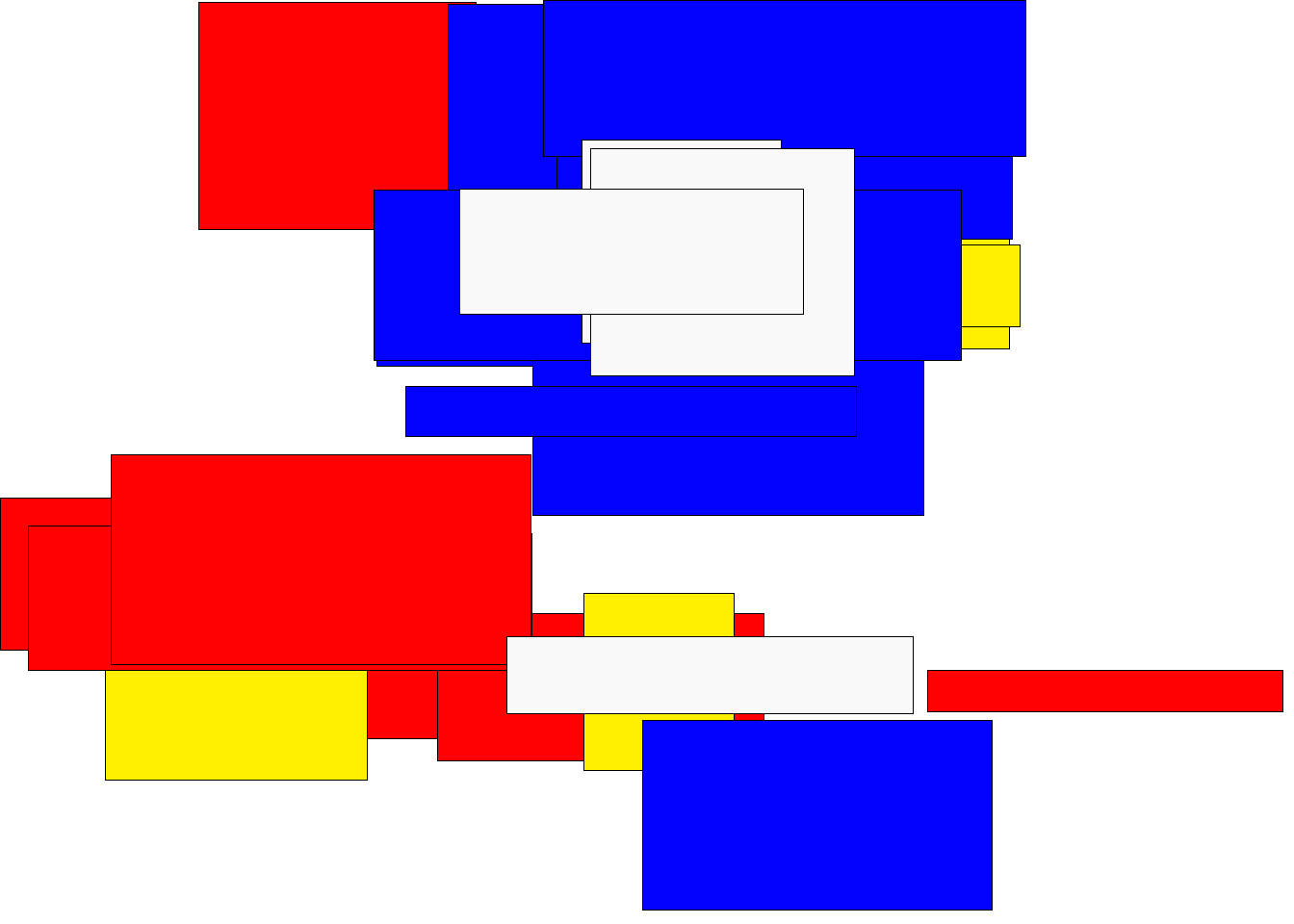
Qué son las marcas gráficas
Las marcas gráficas son elementos gráficos básicos con los que vamos a representar los datos del conjunto de datos, y que en ggplot2 se generan con las diversas funciones geom_.
Podemos distinguir entre las marcas gráficas elementales (puntos, líneas, áreas) y las marcas compuestas, como el boxplot que calcula puntos (estadísticos) y los dibuja como un tipo de caja delimitada por el primer y el tercer cuartil de una variable cuantitativa, a la que se le añade una línea para identificar la mediana, otras líneas para representar los bigotes y, en el caso de que los haya, un punto por cada outlier.
Un problema con el que nos encontraremos muy habitualmente es el problema del overploting, que ocurre cuando una marca tapa a otra. Si al ver el gráfico interpretamos que hay una única marca, donde realmente hay dos (o más), nuestra interpretación será errónea.
Este problema es habitual en conjuntos con muchos datos, pero con dos únicos puntos también puede darse:
tipo <- c("A","B")
x <- c(1,1)
y <- c(1,1)
datos <- as_tibble(tipo = tipo,
x = x,
y = y)
ggplot(datos, aes(x,y, color = tipo)) +
geom_point(size = 10)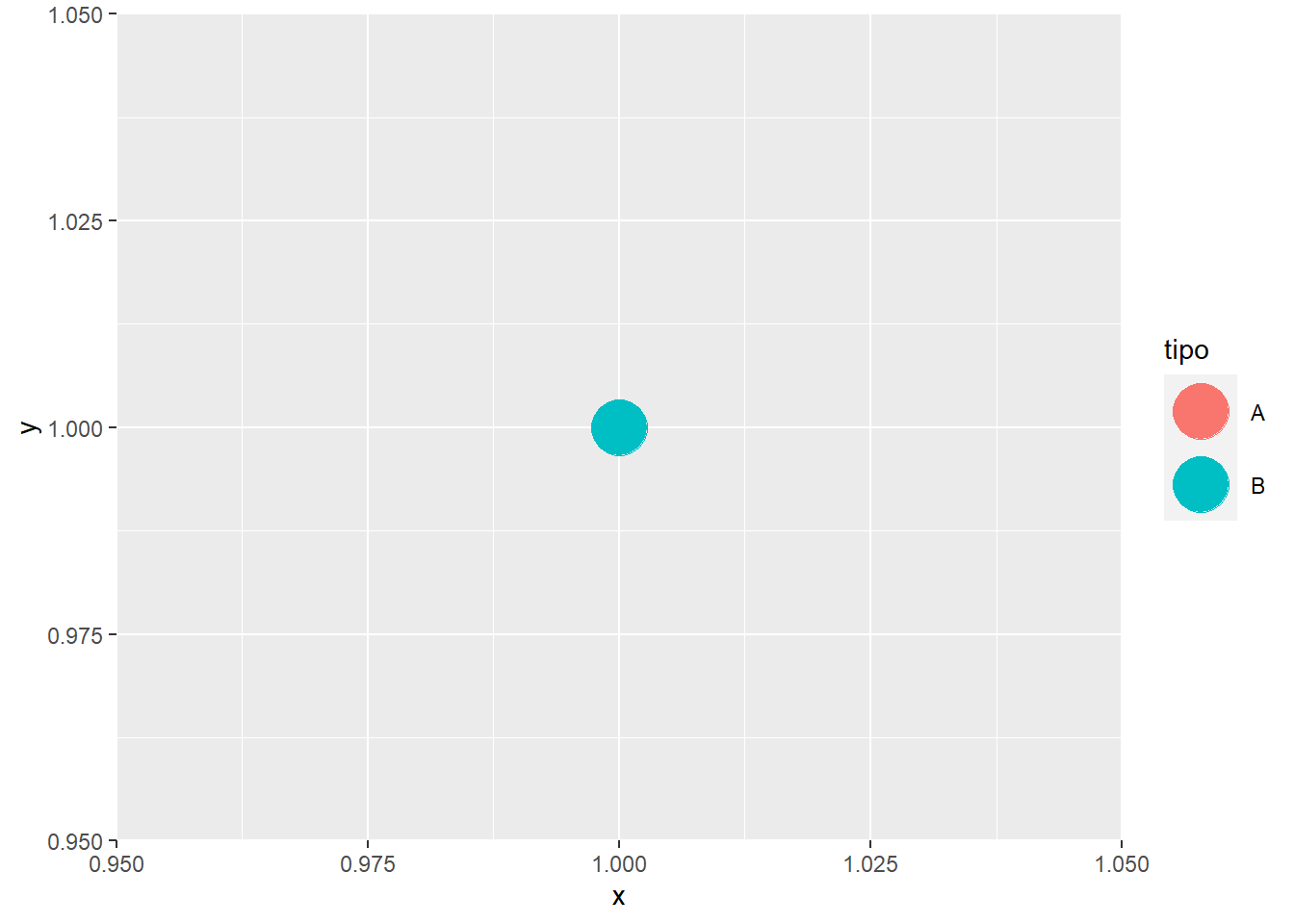
¿Dónde está el punto de tipo A? Oculto, tapado por el punto de tipo B.
position = "jitter" aplica la técnica del jittering, que asigna un desplazamiento aleatorio a las marcas gráficas (podemos jugar con varios parámetros para limitar el desplazamiento a un único eje, o la distancia máxima a la que se puede desplazar una marca desde su punto de origen).
ggplot(datos, aes(x,y, color = tipo)) +
geom_point(position = "jitter", size = 10)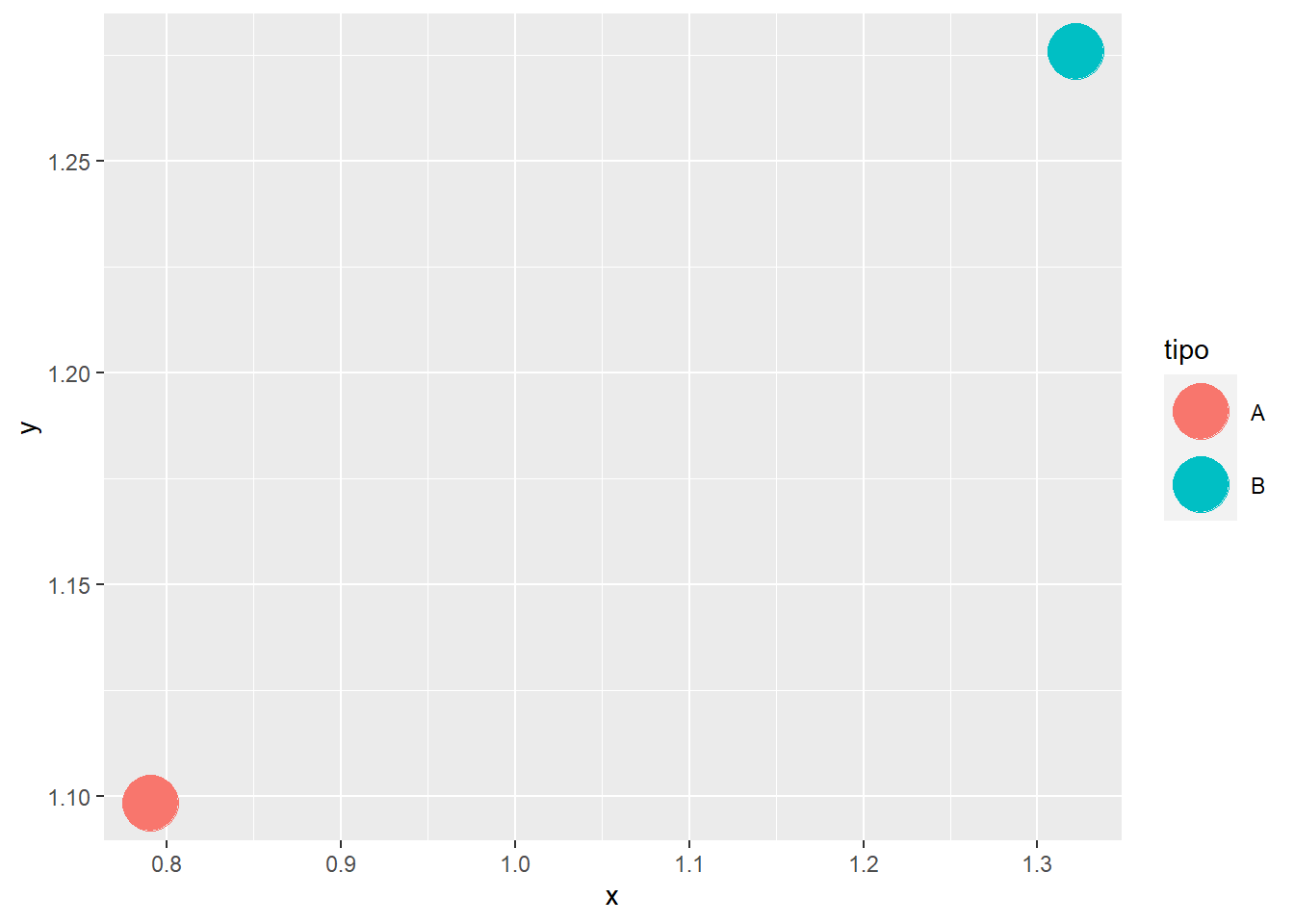
Como veremos en varios ejemplos, este problema es habitual cuando trabajamos con variables discretas.
¿Cuántas marcas se van a dibujar?
Para comprender mejor la interacción entre las variables y los geoms, vamos a intentar adivinar cuántas marcas gráficas se van a generar cuando creamos un gráfico dado.
El número total de marcas que se generarán depende de los siguientes factores:
Geoms usados: algunos geoms como
point,tile… generan una marca por cada fila del conjunto de datos, mientras que otros generan “zonas” (cada una tendrá una marca gráfica) y realizan algún cálculo sobre esas zonas, por defecto contar el número de filas que “caen” en esa zona. Finalmente, tenemosgeomsque generan una “marca compuesta”, comoboxplot(que computa varios estadísticos y los resume en un rectángulo, unas líneas, y puntos en el caso de outliers extremos) oviolin. De estos últimos hablaremos en otro post.En el caso de los
geomscuyosstatsrealizan cuentas (histogram,bin2d,hex), argumentos comobinsobinwidthdiscretizan la(s) variable(s) continua(s) y establecen el número de marcas gráficas que se generarán.
Para todos los ejemplos vamos a usar el conjunto de datos mpg de ggplot2, que tiene 234 filas y 11 columnas.
library(ggplot2)
head(mpg)## # A tibble: 6 x 11
## manufacturer model displ year cyl trans drv cty hwy fl class
## <chr> <chr> <dbl> <int> <int> <chr> <chr> <int> <int> <chr> <chr>
## 1 audi a4 1.8 1999 4 auto(l5) f 18 29 p compa~
## 2 audi a4 1.8 1999 4 manual(m5) f 21 29 p compa~
## 3 audi a4 2 2008 4 manual(m6) f 20 31 p compa~
## 4 audi a4 2 2008 4 auto(av) f 21 30 p compa~
## 5 audi a4 2.8 1999 6 auto(l5) f 16 26 p compa~
## 6 audi a4 2.8 1999 6 manual(m5) f 18 26 p compa~geom_point
Este geom dibuja un punto; para poder hacerlo, nos pedirá dos variables de posición (x e y), aunque como veremos podemos pasarle valores constantes. También podemos modificar otros canales gráficos (color, tamaño…), pero no influyen en el número de marcas total que se dibujan.
NOTA: en este aspecto, el funcionamiento de ggplot y de Tableau es opuesto. Si no mapeamos ninguna variable discreta, geom_point()(y otros geoms) crearán una marca gráfica por cada fila del conjunto de datos, mientras que en Tableau el comportamiento es justo el contrario: si no mapeamos ninguna variable discreta (dimensión), Tableau agregará los datos a un único punto. Por este motivo, si añadimos una variable discreta a color (por ejemplo), en ggplot seguiremos teniendo el mismo número de marcas (ya que estamos trabajando al nivel más desagregado de los datos), mientras que en Tableau se crearán más marcas (una por cada nivel de la variable llevada a color), ya que estaremos desagregando los datos.
Variables continuas
geom_point genera un punto por cada fila del conjunto de datos.
ggplot(mpg, aes(x = cty)) +
geom_point()## Error: geom_point requires the following missing aesthetics: y
Por defecto geom_point() nos pide dos variables, pero podemos trabajar con una sola, asignando un valor constante a la segunda variable de posicionamiento.
ggplot(mpg, aes(x = cty, y = 0)) +
geom_point()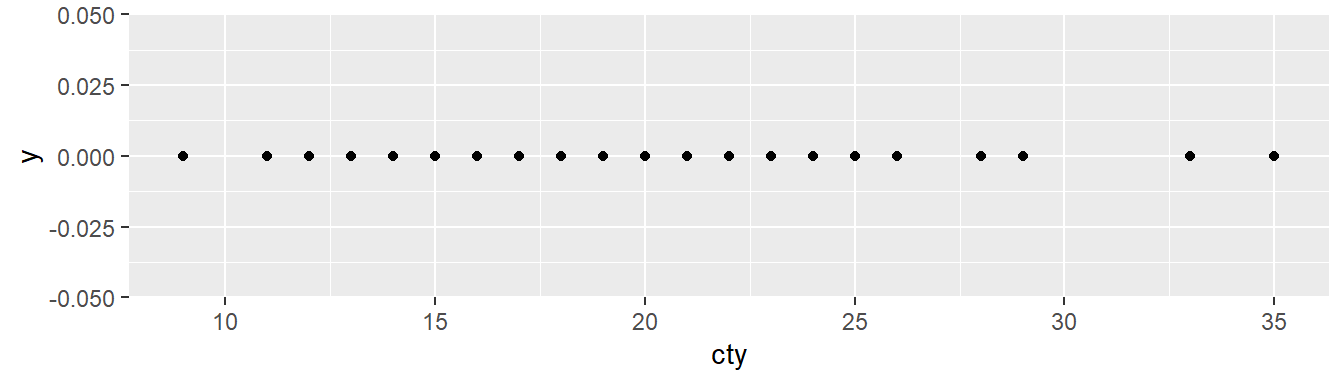
Como ha hemos mencionado, el conjunto de datos consta de 234 filas, y geom_point() dibuja un punto por cada una de ellas. ¿Dónde están los puntos que faltan?
Estamos ante un claro caso de overploting. Si aplicamos un pequeño desplazamiento aleatorio a cada punto, podremos ver que los puntos estaban ahí desde el principio.
ggplot(mpg, aes(x = cty, y = 0)) +
geom_point(position = "jitter")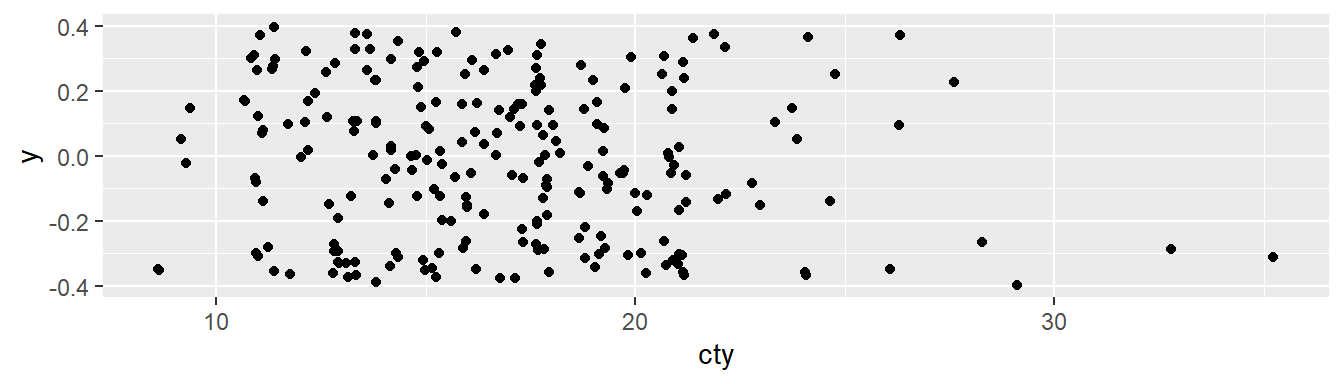
Si asignamos dos variables continuas (que es lo que pide geom_point por defecto, obtenemos un gráfico de dispersión o scatterplot:
ggplot(mpg, aes(cty, hwy)) +
geom_point()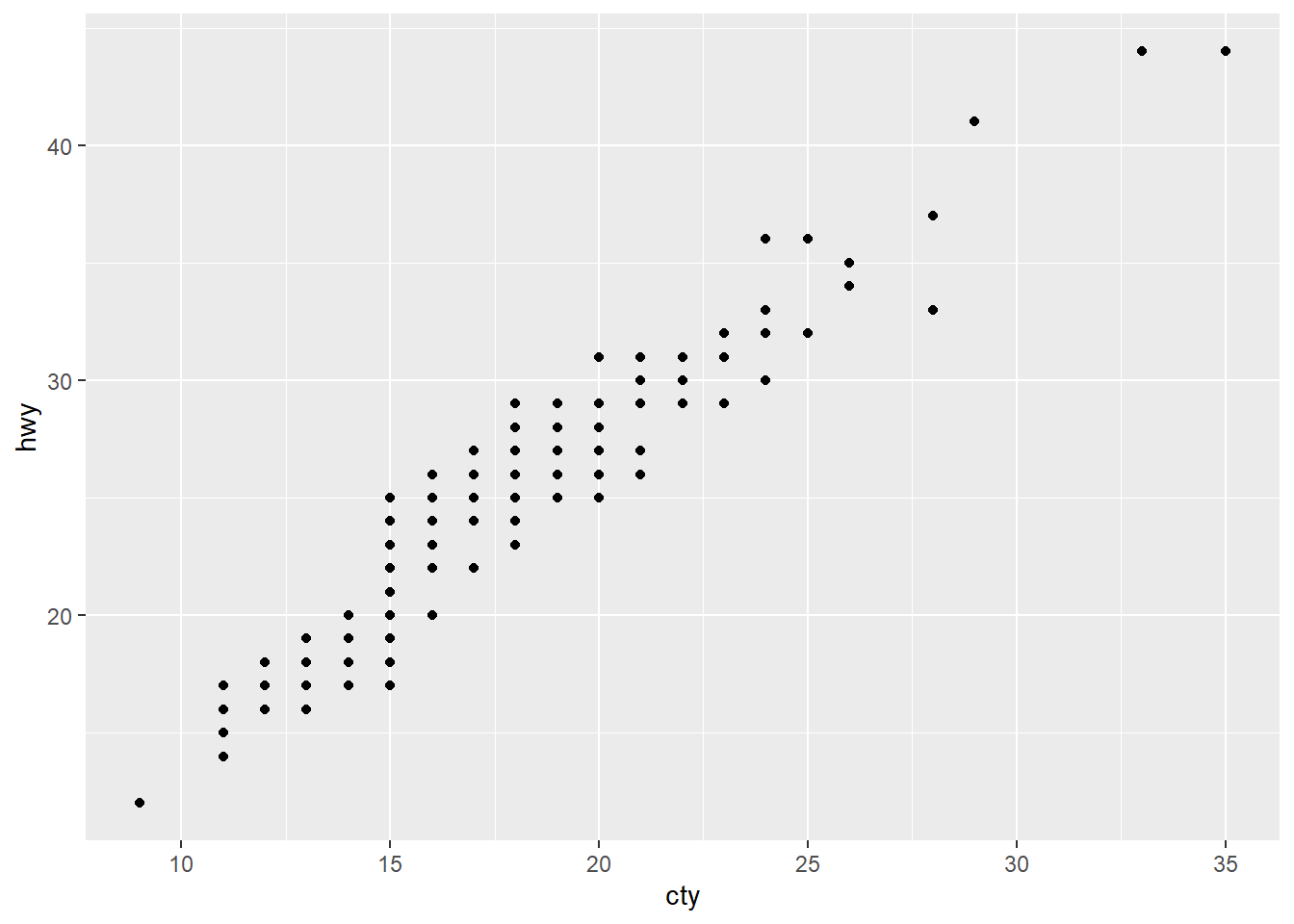
En este caso volvemos a tener overploting, como podemos apreciar al aplicar la técnica de jittering (podemos fijarnos, por ejemplo, en el en el punto 8,12 -más o menos- del gráfico original).
ggplot(mpg, aes(cty, hwy)) +
geom_point(position = "jitter")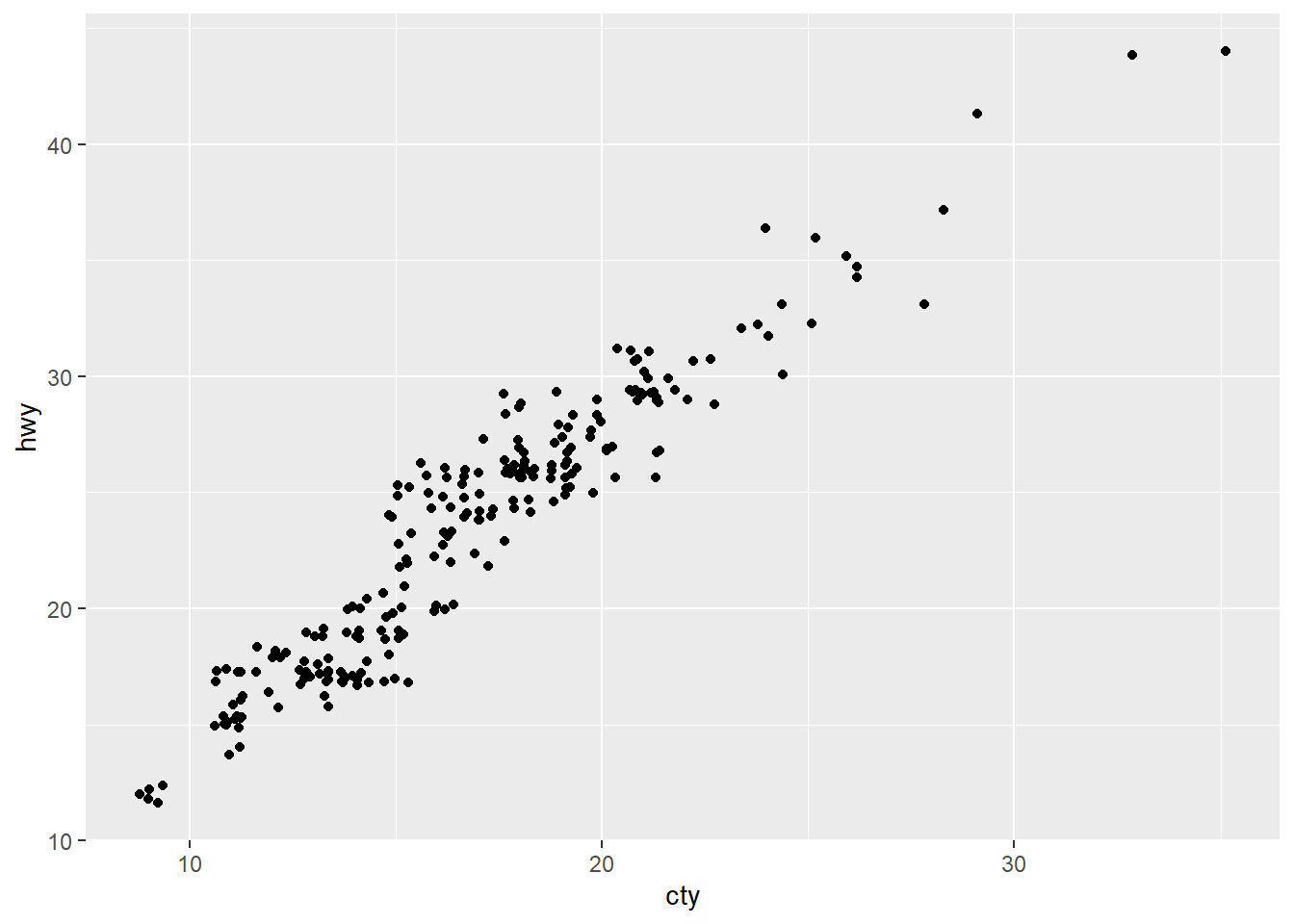
Variables discretas
ggplot(mpg, aes(x = drv)) +
geom_point()## Error: geom_point requires the following missing aesthetics: y
ggplot(mpg, aes(x = drv, y = 0)) +
geom_point()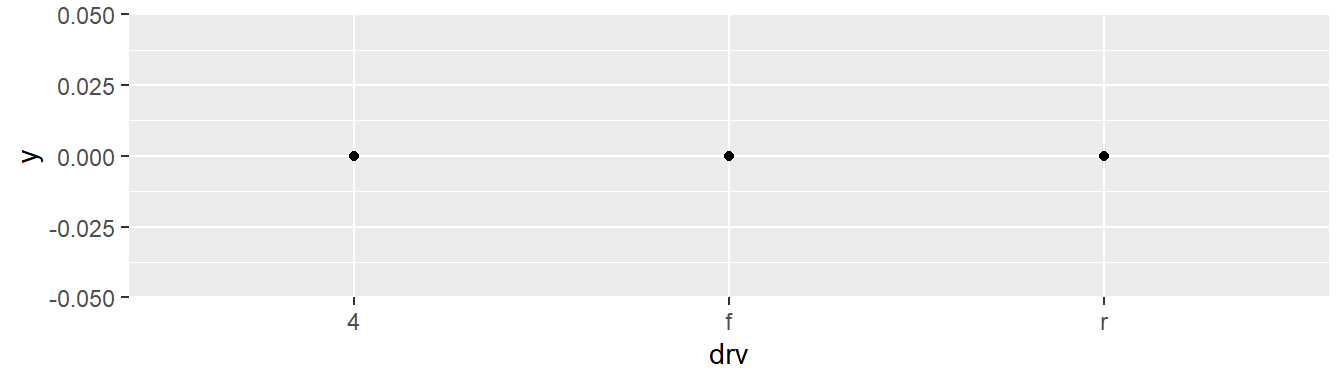
El problema del overploting se acentúa cuando trabajamos con variables discretas de pocos niveles.
ggplot(mpg, aes(x = drv, y = 0)) +
geom_point(position = "jitter")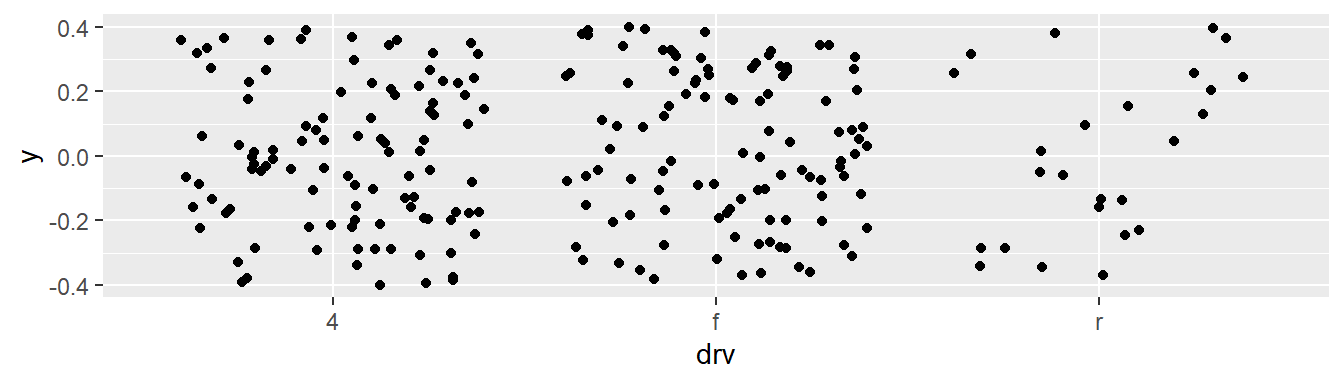
ggplot(mpg, aes(x = drv, y = class)) +
geom_point()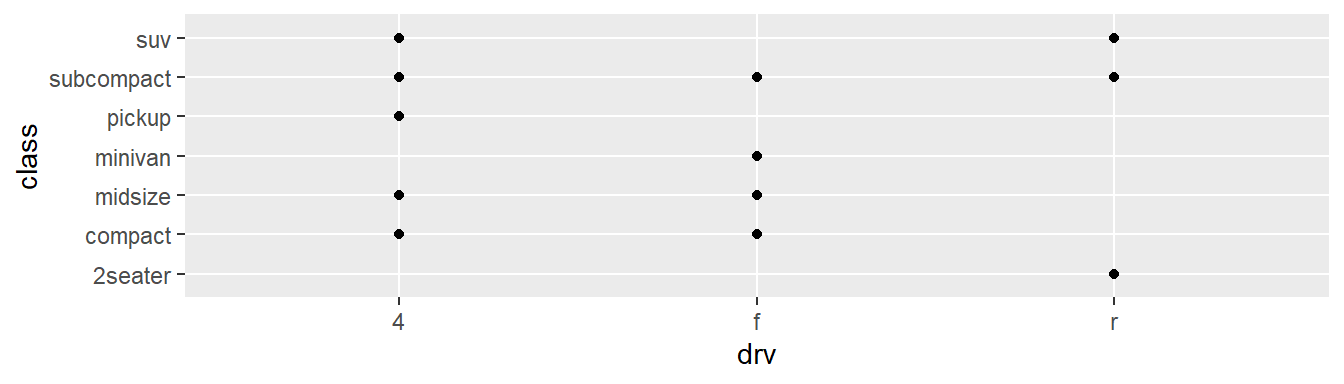
ggplot(mpg, aes(x = drv, y = class)) +
geom_point(position = "jitter")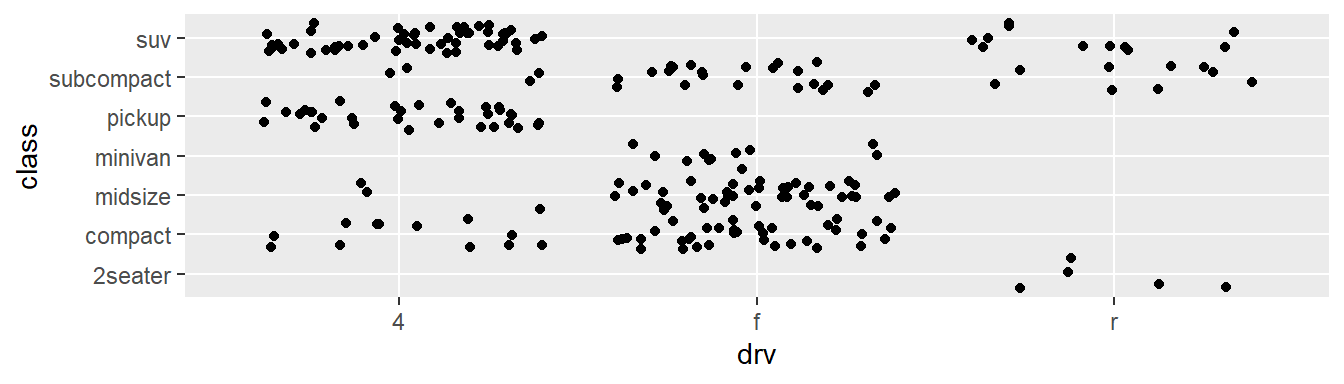
Variables discretas y continuas
ggplot(mpg, aes(x = cty, y = class)) +
geom_point()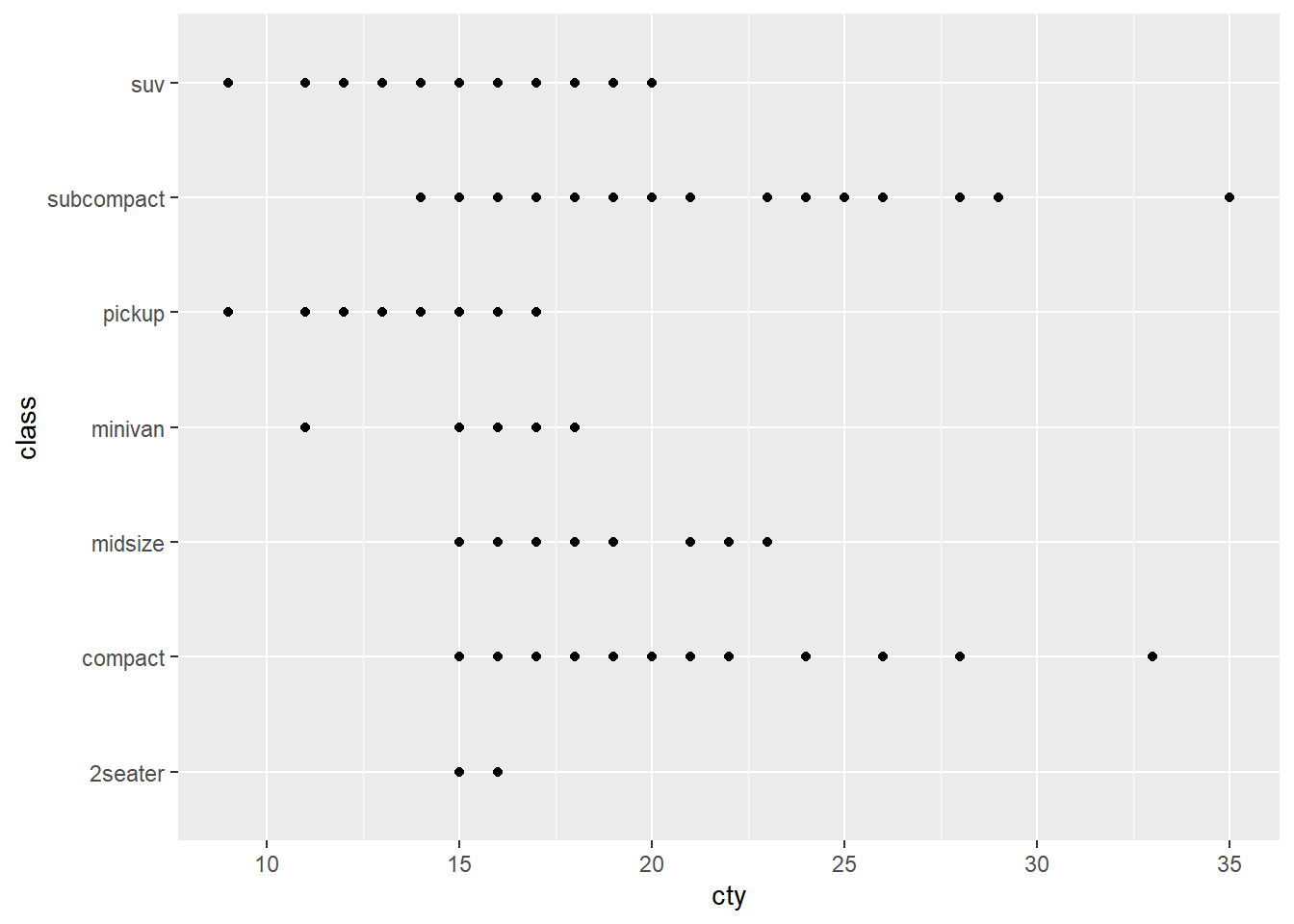
ggplot(mpg, aes(x = cty, y = class)) +
geom_point(position = "jitter")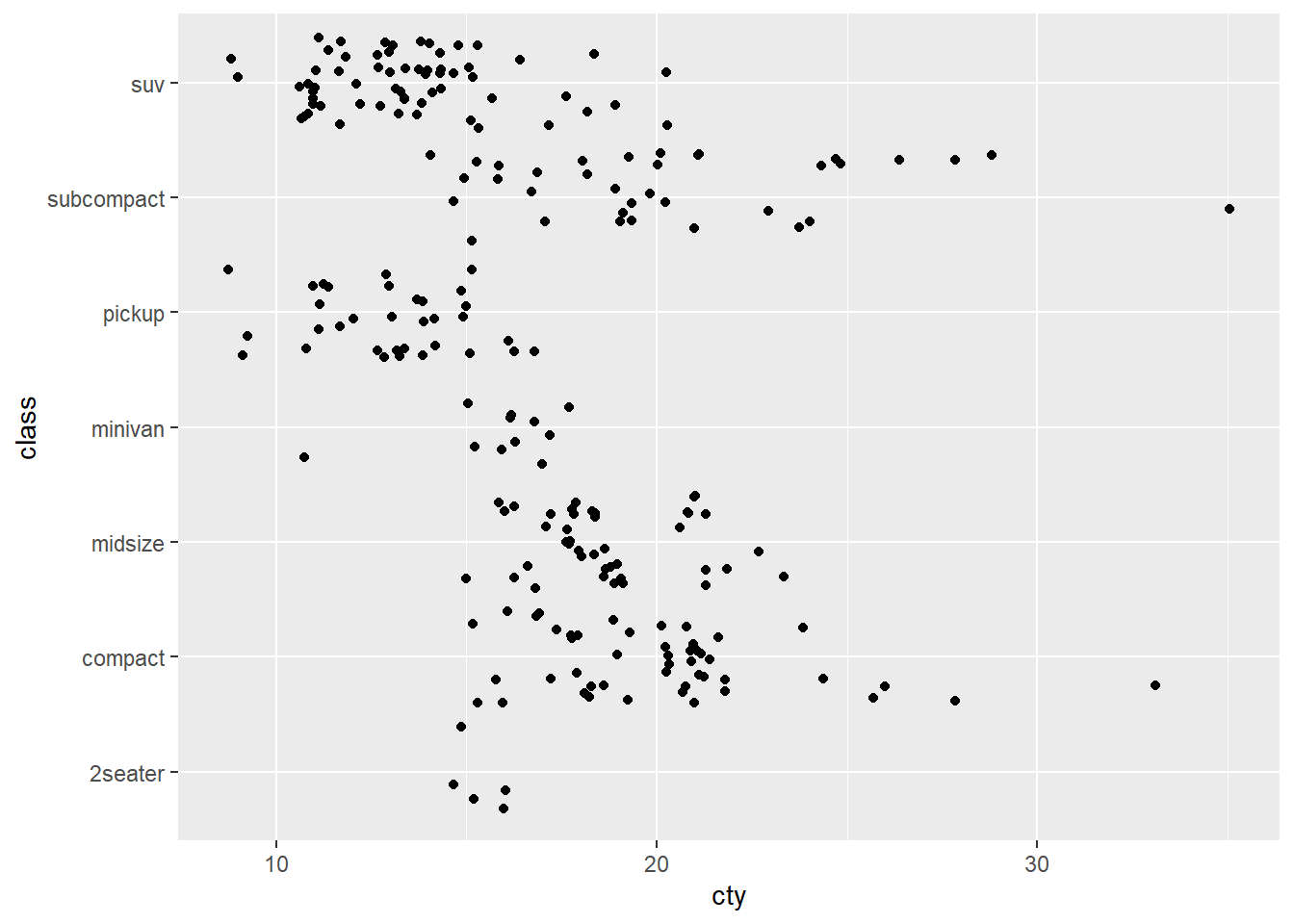
geom_histogram, geom_bar y geom_col
Aunque la apariencia final de estos geoms pueda ser idéntica, el funcionamiento interno no lo es (de otra forma no habrían creado los tres geoms)
En su configuración por defecto:
- Los histogramas funcionan con una única variable continua, que clasifican a partir de un argumento que puede indicar el usuario (por defecto ggplot crea 30 clases, que pueden o no contener datos, por lo que el número de marcas gráficas final será igual o menor a dicho argumento)
- Las barras funcionan con una única variable discreta; se crea una marca por cada nivel. La longitud de la barra depende del número de elementos que se cuenten en cada nivel.
- Las columnas combinan una variable discreta con una continua. Se crea una marca por cada nivel de la variable discreta. La forma de trabajo más habitual consiste en agregar primero los datos al nivel que nos interese (por ejemplo, suma de ventas por departamento) y luego llevar los datos agregados a ggplot. La variable discreta nos dará el número de marcas gráficas, mientras que la cuantitativa indica la longitud de las columnas.
- Si usamos dos o más variables discretas, el número de marcas será el obtenido al cruzar los niveles de las variables discretas, siempre que todos los cruces tengan algún dato.
ggplot(mpg, aes(cty)) +
geom_histogram()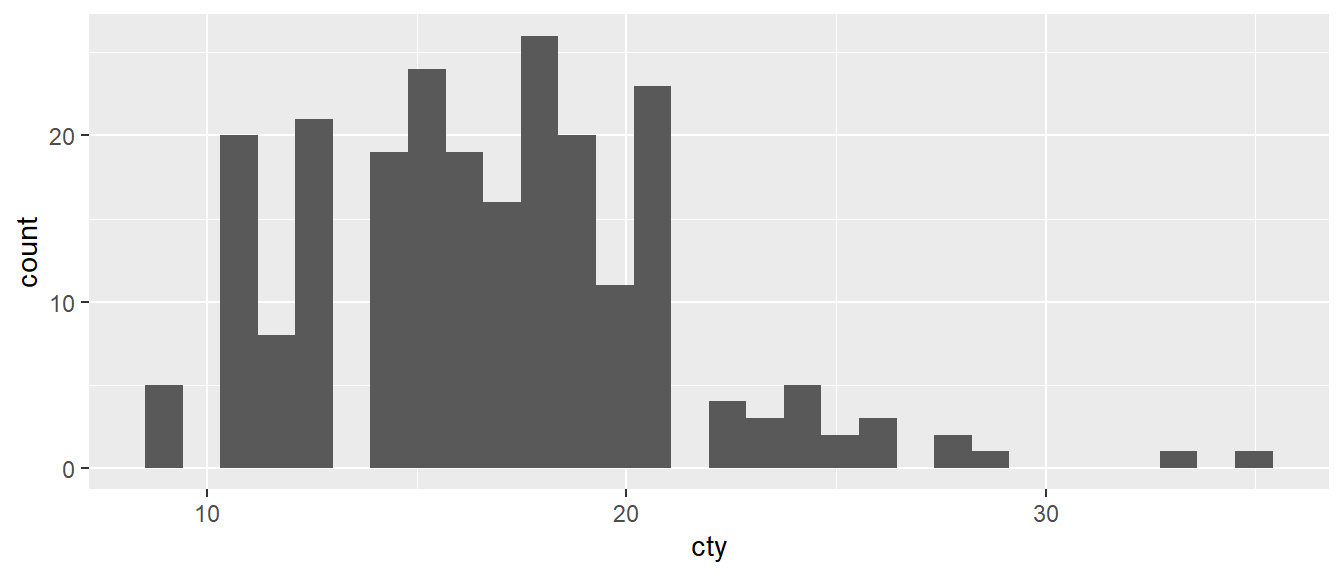
ggplot(mpg, aes(class)) +
geom_histogram()## Error: StatBin requires a continuous x variable: the x variable is discrete.Perhaps you want stat="count"?
ggplot(mpg, aes(cty)) +
geom_bar()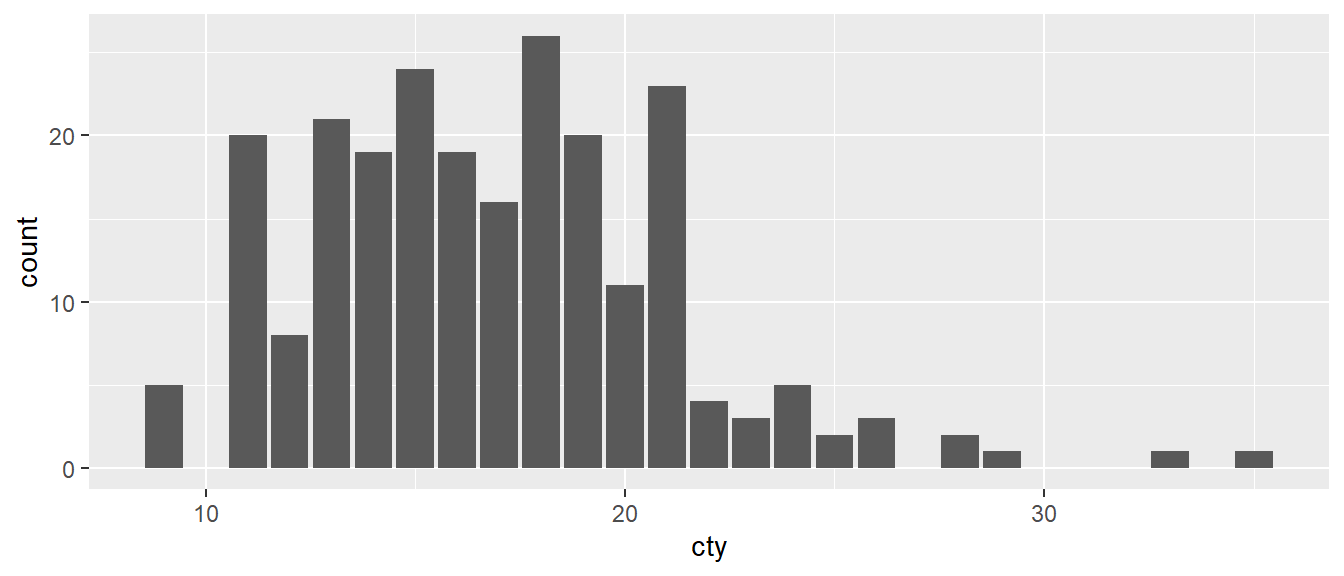
En este caso, la variable continua cty no ha sido clasificada, sino que cada valor único tiene su propia columna.
sort(unique(mpg$cty))## [1] 9 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 28 29 33 35ggplot(mpg, aes(class)) +
geom_bar()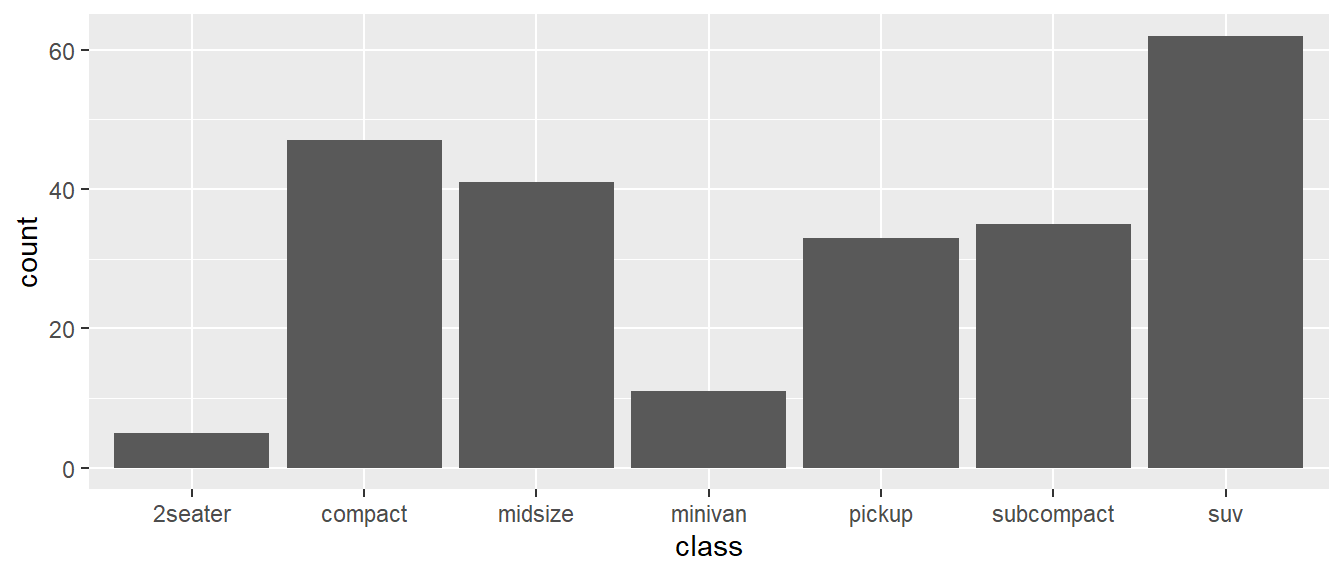
ggplot(mpg, aes(cty, class)) +
geom_histogram()## Error: stat_bin() can only have an x or y aesthetic.
ggplot(mpg, aes(cty, class)) +
geom_bar()## Error: stat_count() can only have an x or y aesthetic.
ggplot(mpg, aes(cty, fill = drv)) +
geom_histogram()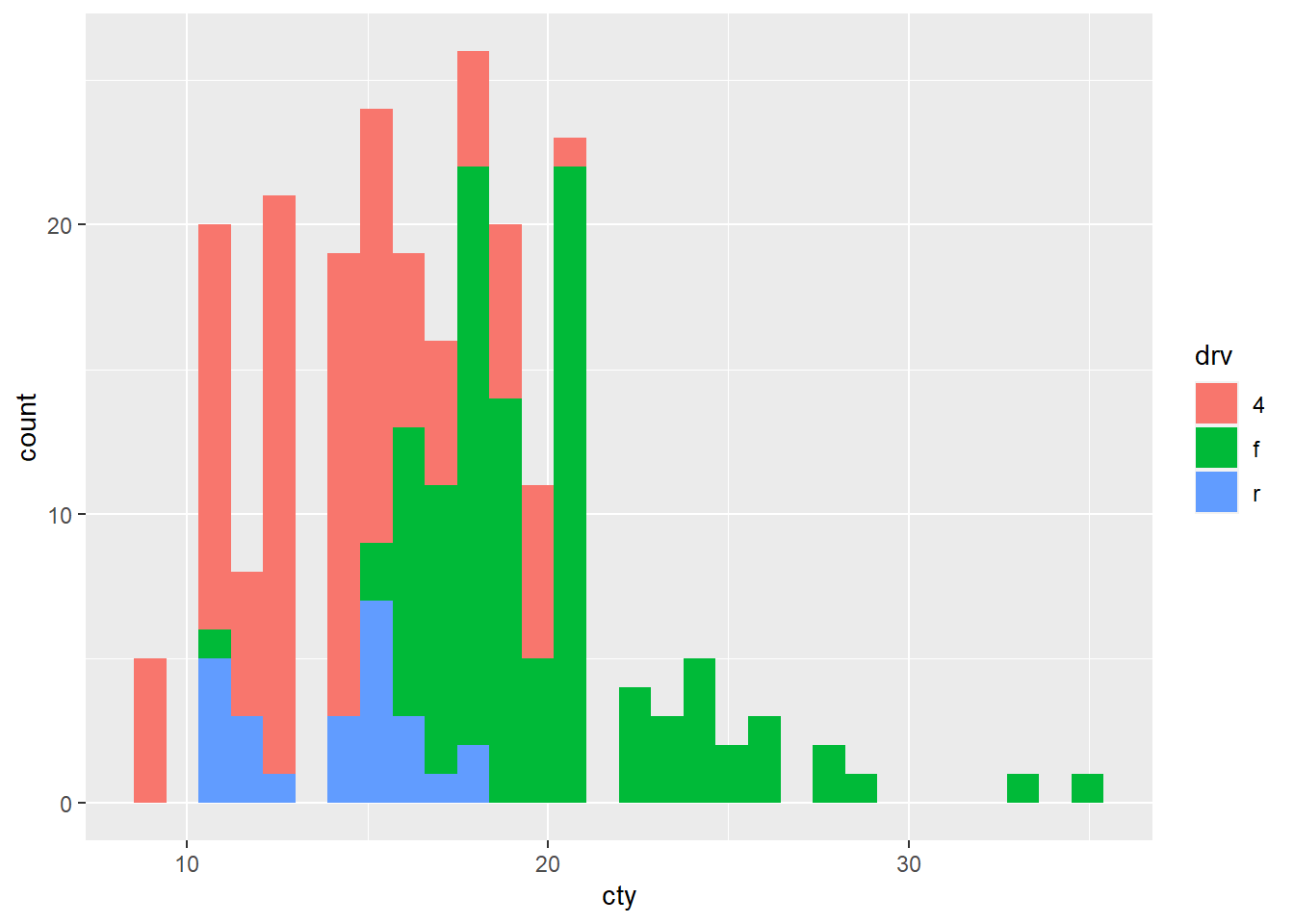
ggplot(mpg, aes(class, fill = drv)) +
geom_bar()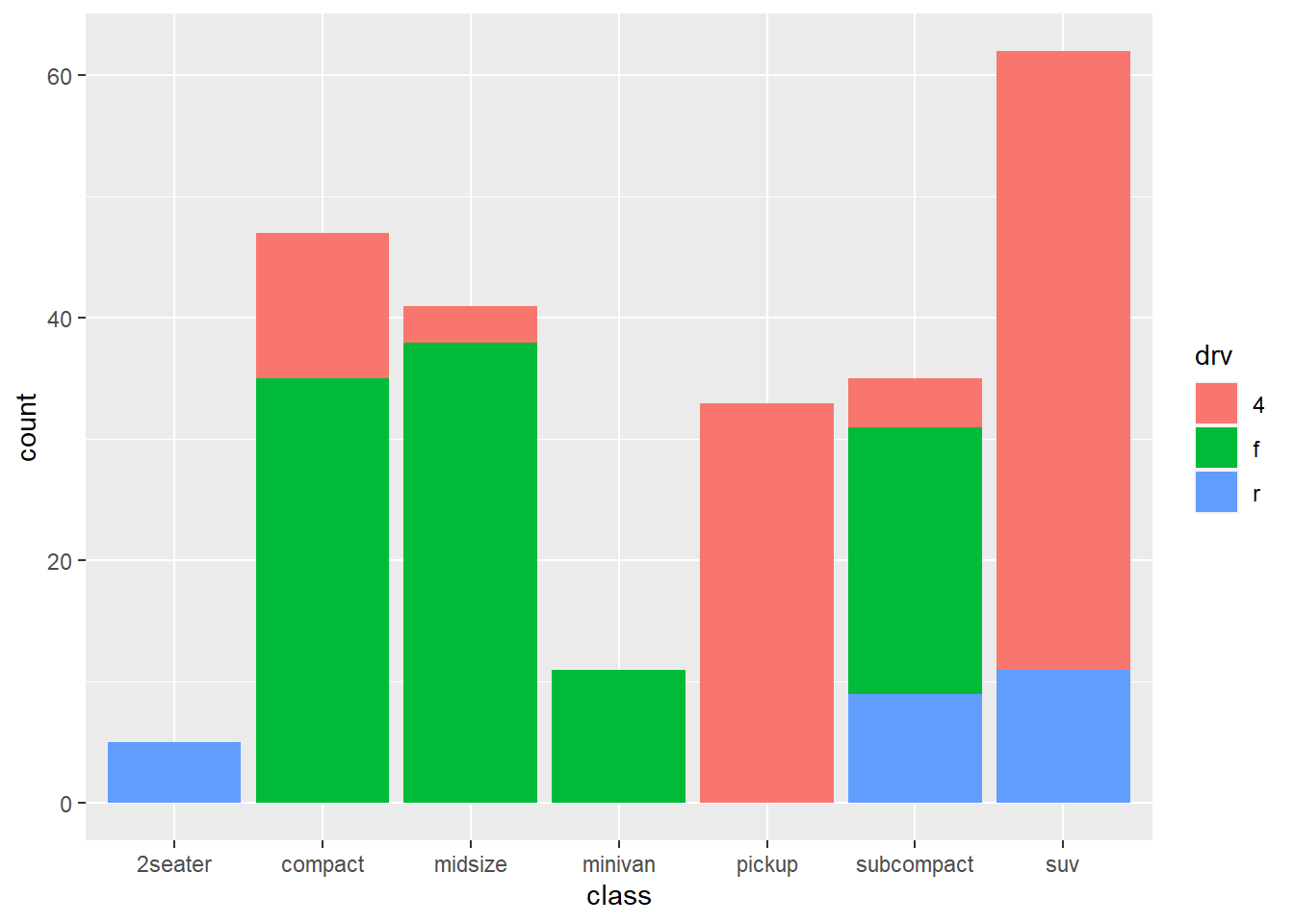
ggplot(mpg, aes(class, fill = cty)) +
geom_bar()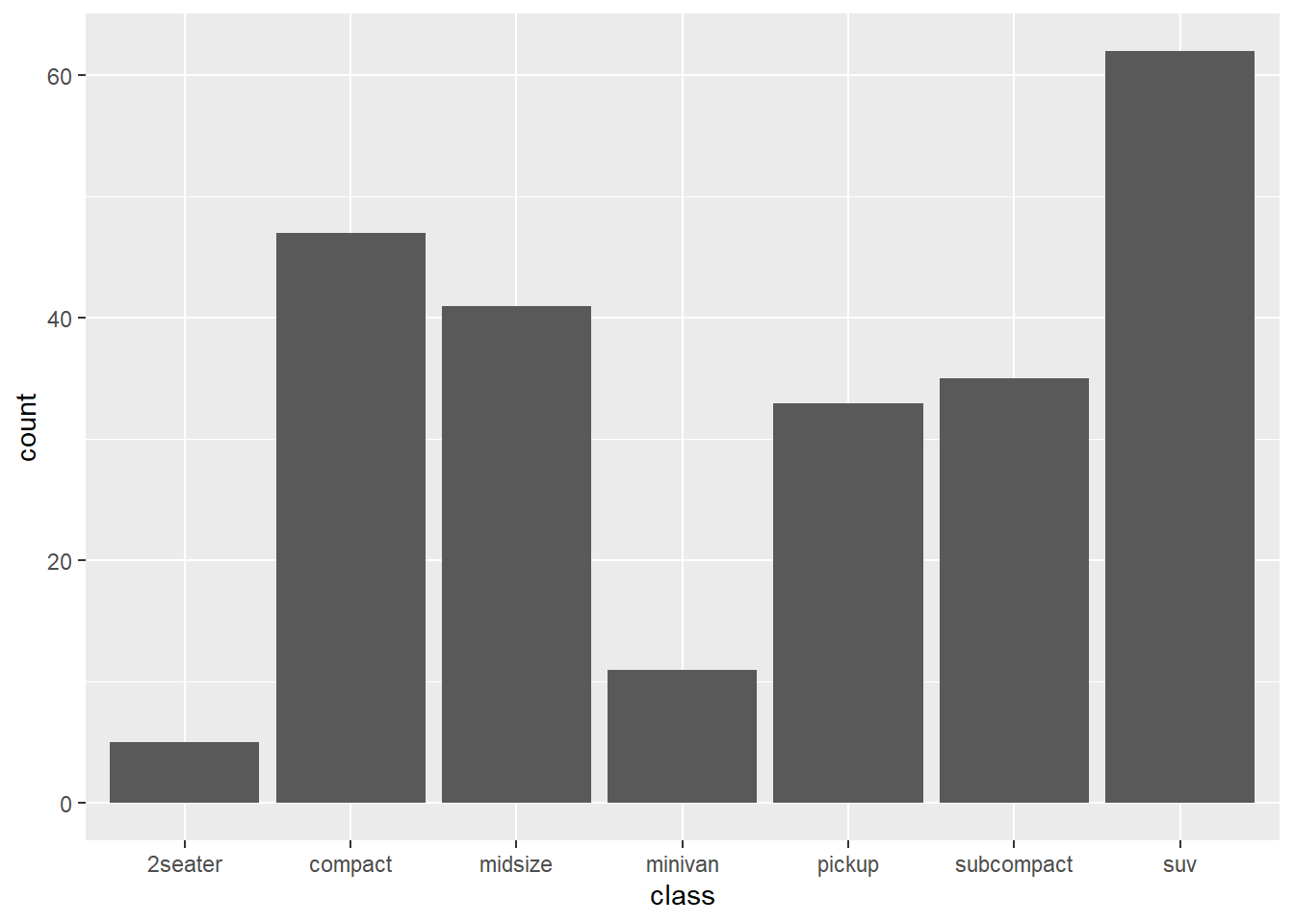
ggplot(mpg, aes(x = manufacturer)) +
stat_summary(aes(y = hwy), fun = median, geom = "col")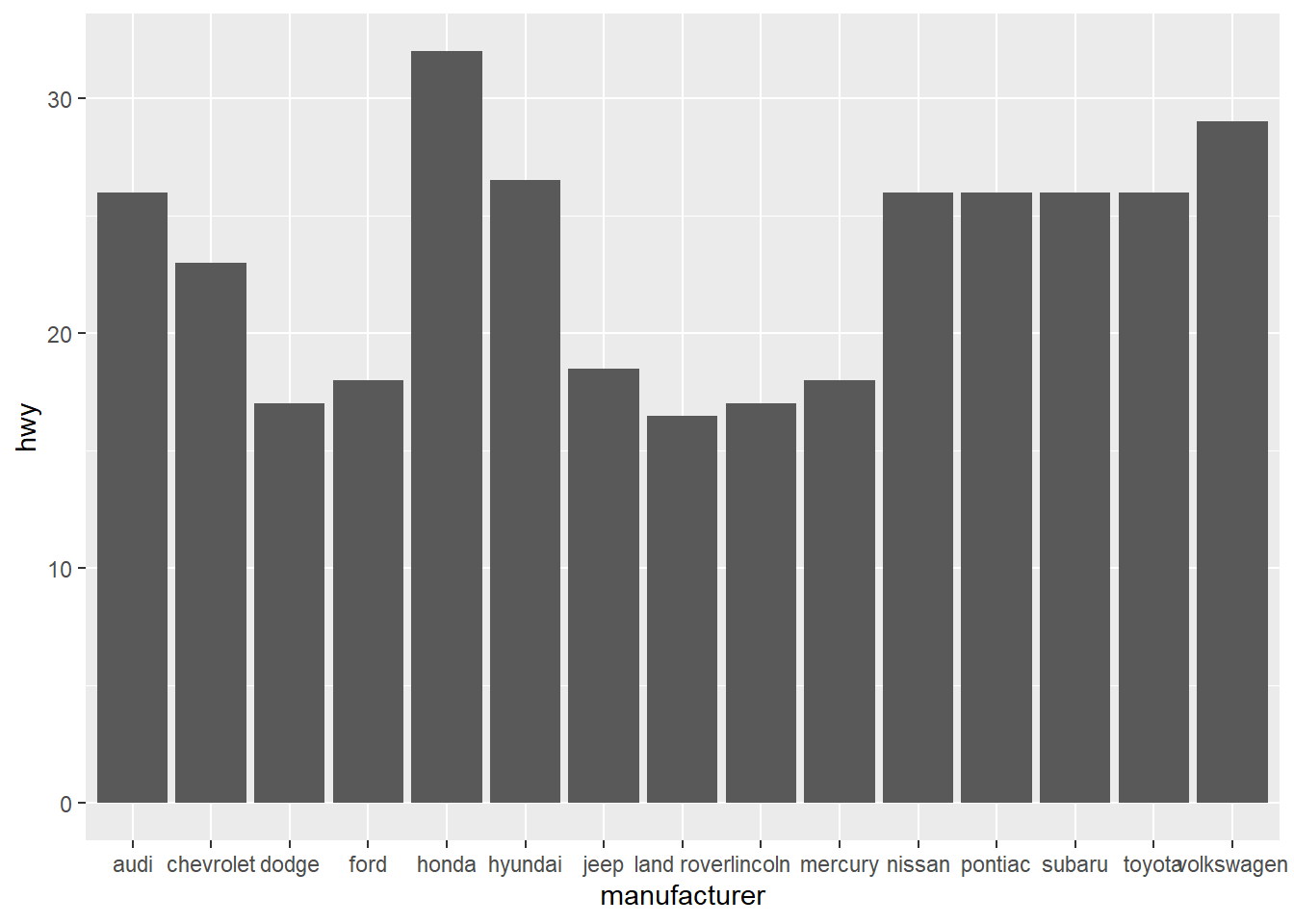
geom_tile(), geom_raster(), geom_bin2d() y geom_hex()
Al principio del post he comentado que iba a tratar sobre puntos y barras, y que dejo las líneas y áreas para otro post.
¿A qué viene hablar aquí de rectángulos y hexágonos, y no dejarlo para el post en el que trabajaremos con áreas?
La razón es muy simple: a pesar de que la forma dibujada sea un rectángulo, los datos necesarios para calcular la posición son los mismos que necesitamos para dibujar un punto, a saber, x e y.
De hecho, en todos los casos (salvo geom_tile(), al que podemos variar altura y anchura) todas las marcas de estos geoms van a tener el mismo tamaño.
geom_rect(), por el contrario, necesita la posición de sus cuatro vértices, no del centro. Aunque con geom_rect() y geom_tile() podemos llegar a dibujar el mismo gráfico, los datos necesarios en cada uno de ellos son distintos (en este post explico cómo crear un gráfico de barras apiladas con geom_rect() -normalmente usaríamos geom_bar() o geom_col()-).
Para variables continuas, geom_tile() funciona como geom_bar() y geom_bin2d() lo hace como geom_histogram(), pero en ambos casos en dos dimensiones. Particionan el espacio (por valores únicos o bins, respectivamente); además, para cada localización generada geom_bin2d() y geom_hex() hacen un recuento de filas, que mapean con el aesthetic fill.
Dos variables continuas
ggplot(mpg, aes(cty, hwy)) +
geom_tile(color = "white")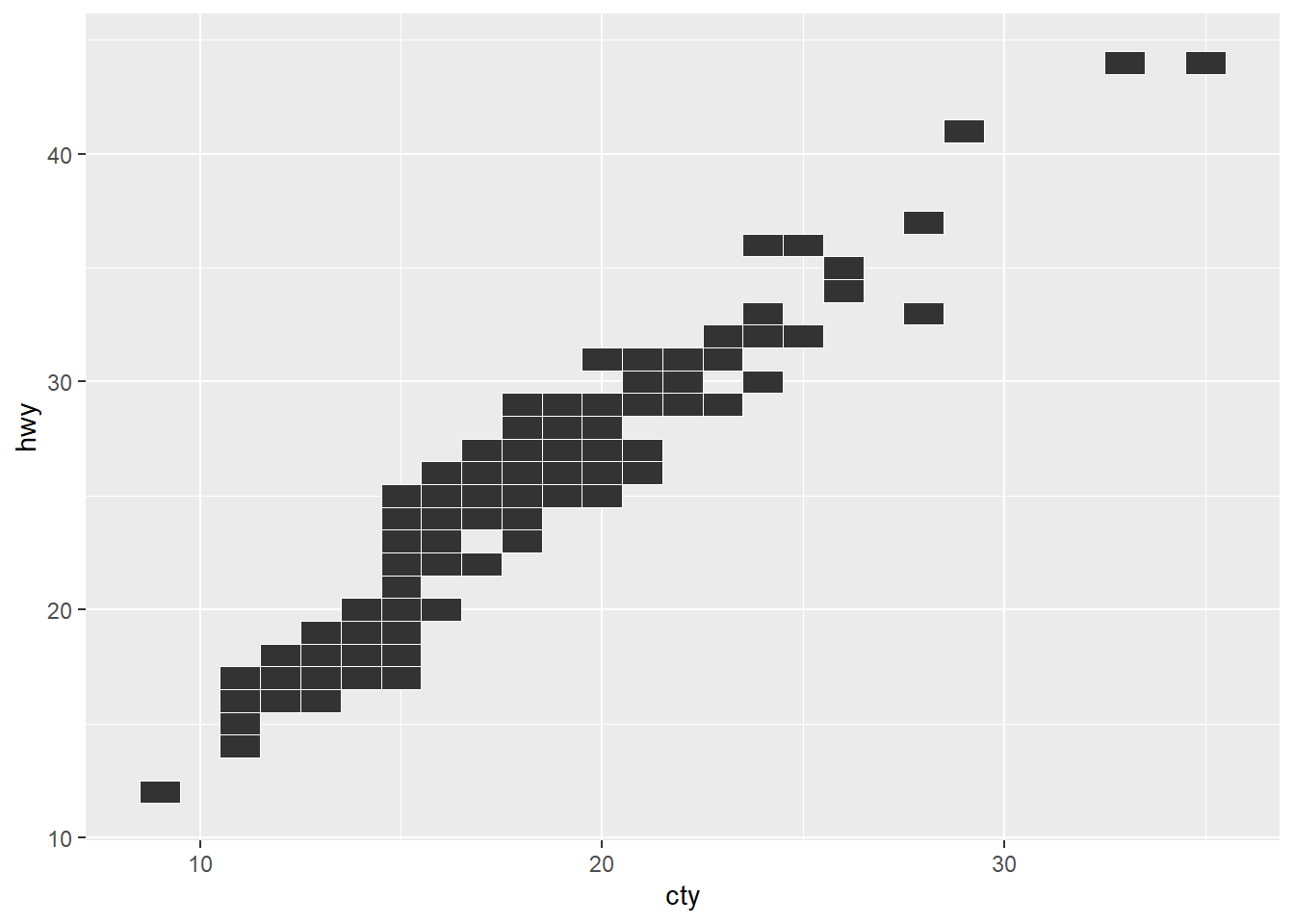
ggplot(mpg, aes(cty, hwy)) +
geom_bin2d(color = "white")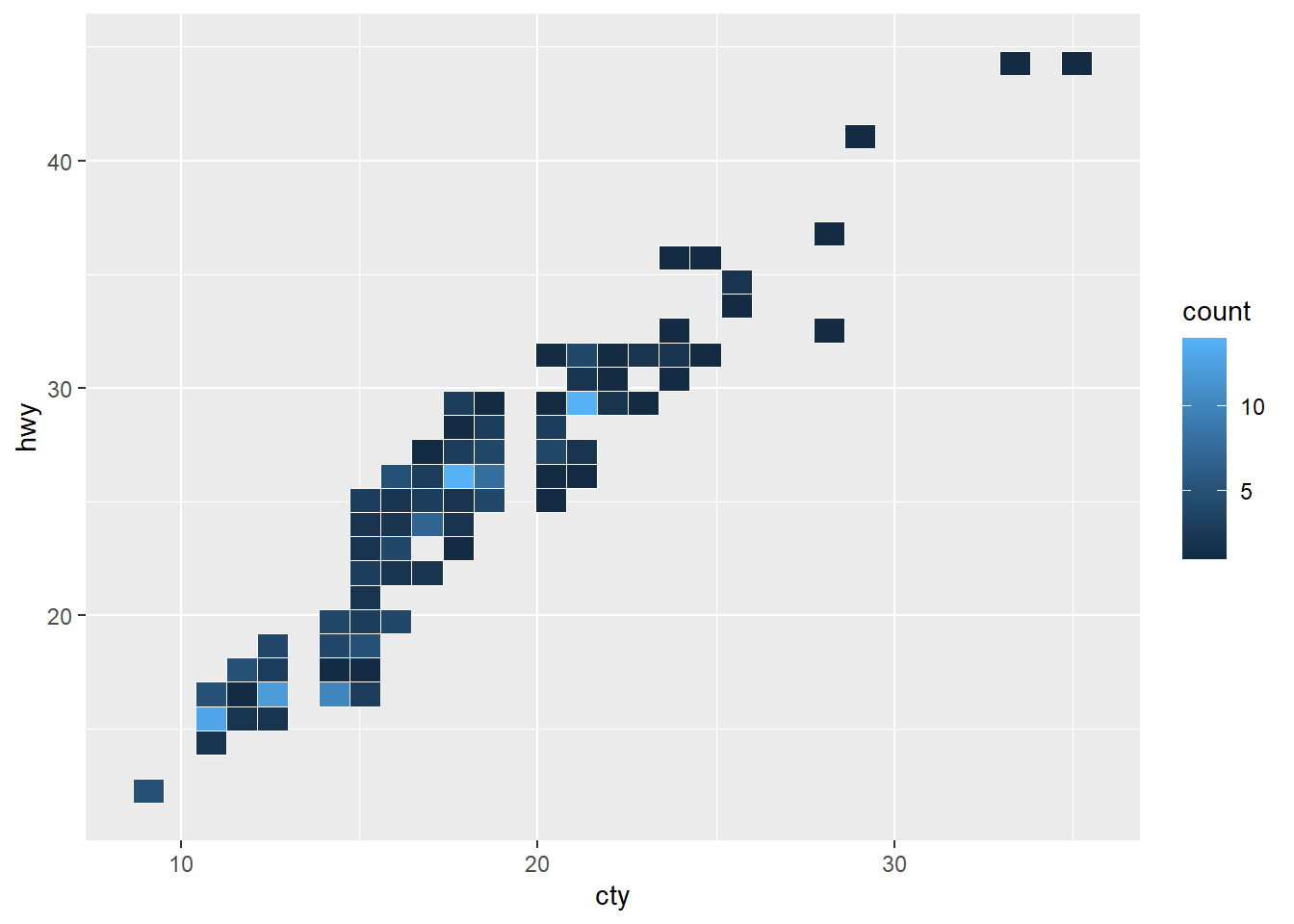
ggplot(mpg, aes(cty, hwy)) +
geom_hex(color = "white")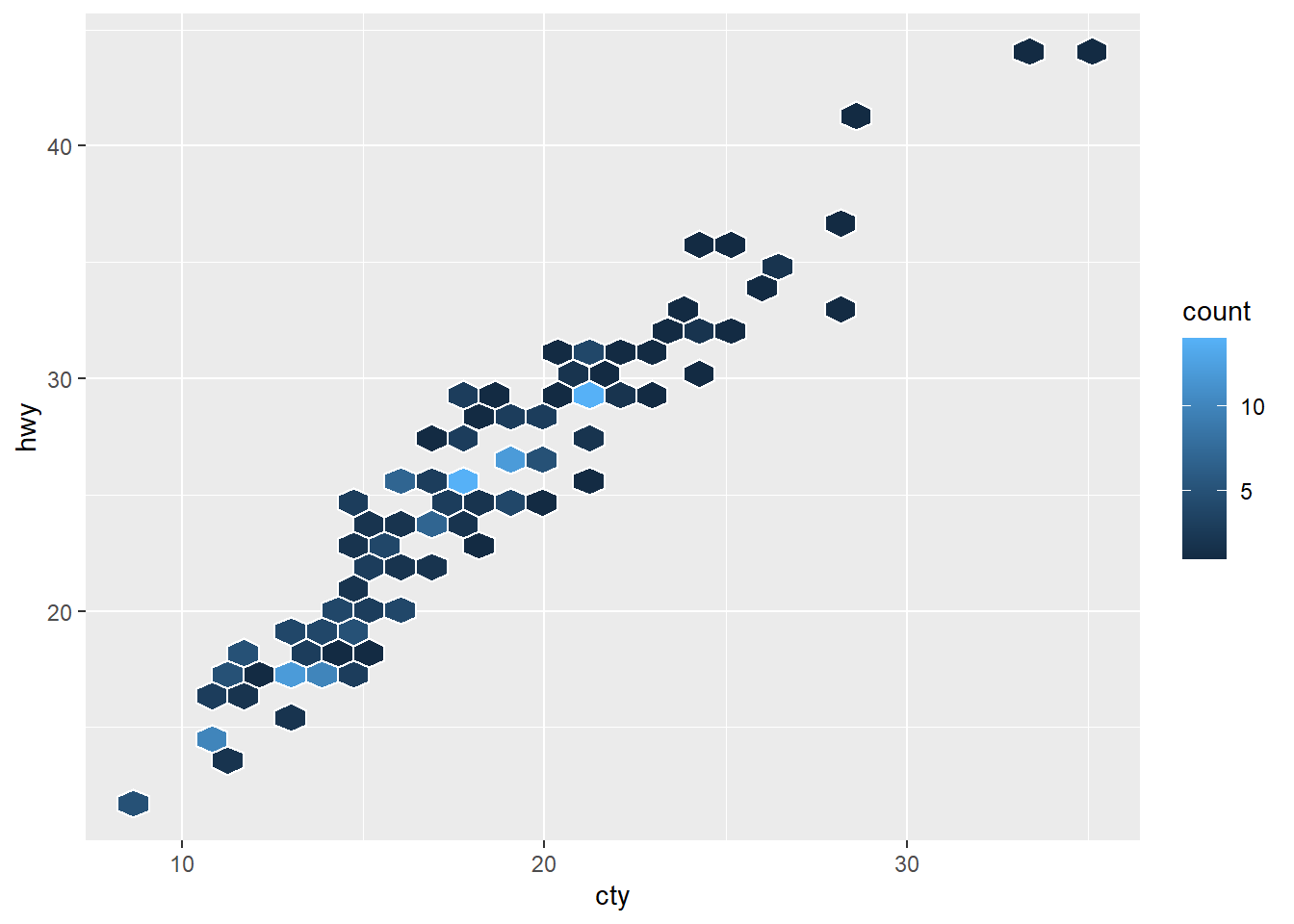
Variables continuas y discretas
ggplot(mpg, aes(cty, drv)) +
geom_tile(color = "white")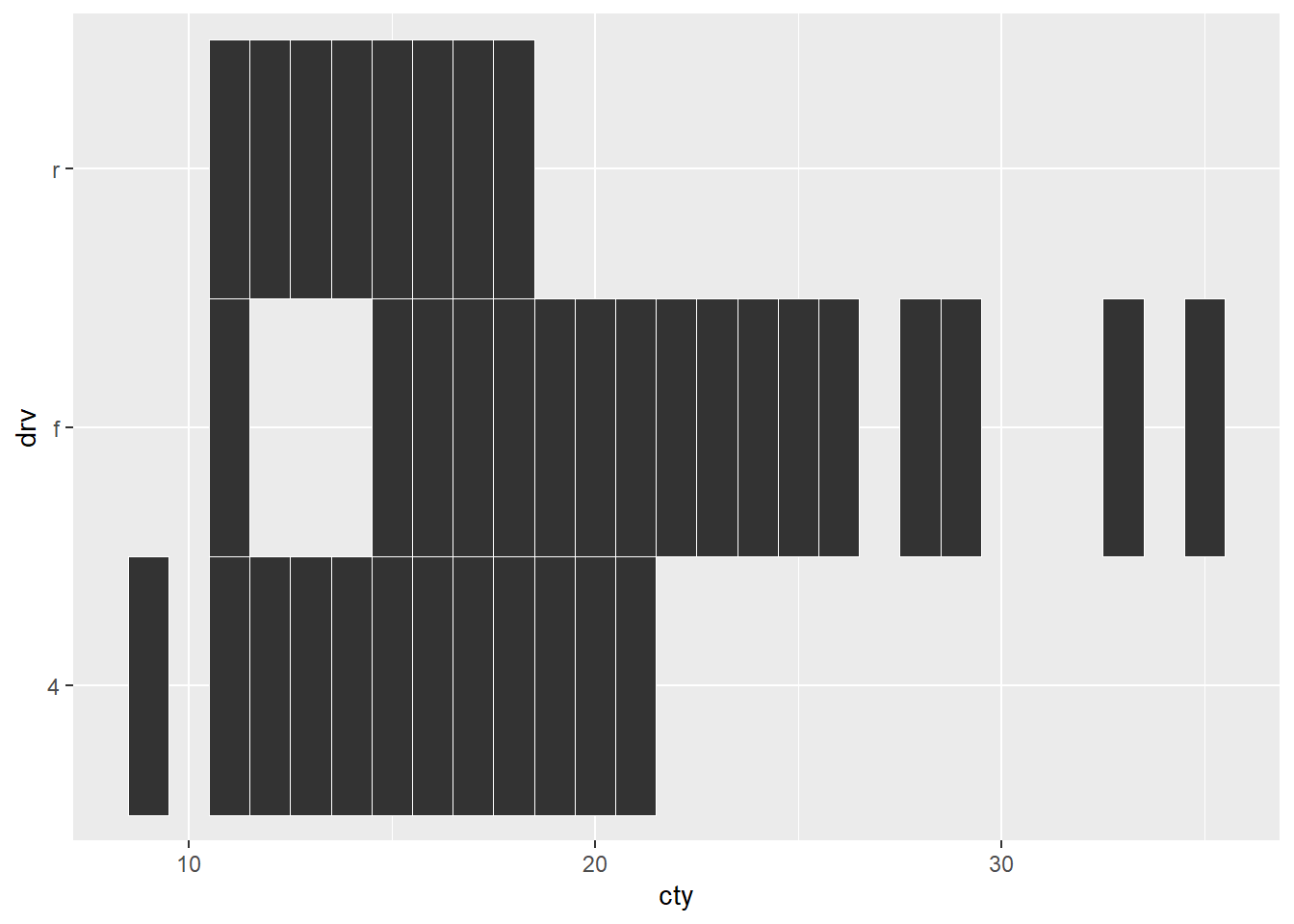
ggplot(mpg, aes(cty, trans)) +
geom_hex(color = "white")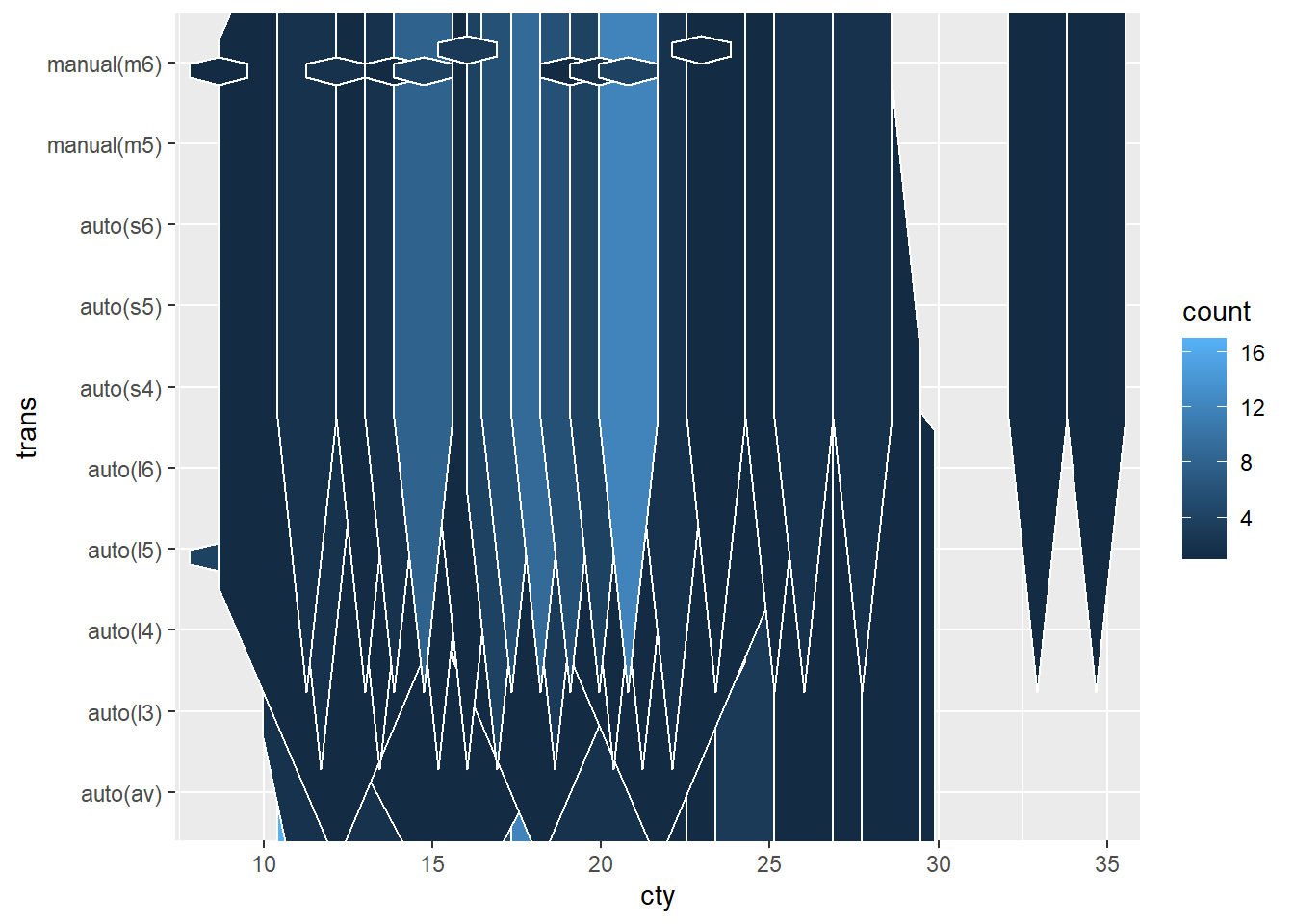
Curiosamente geom_hex() no muestra un mensaje de error al mapearle una variable categórica, pero obviamente el resultado no es el esperado.
Dos variables discretas
ggplot(mpg, aes(drv, class)) +
geom_tile(color = "white")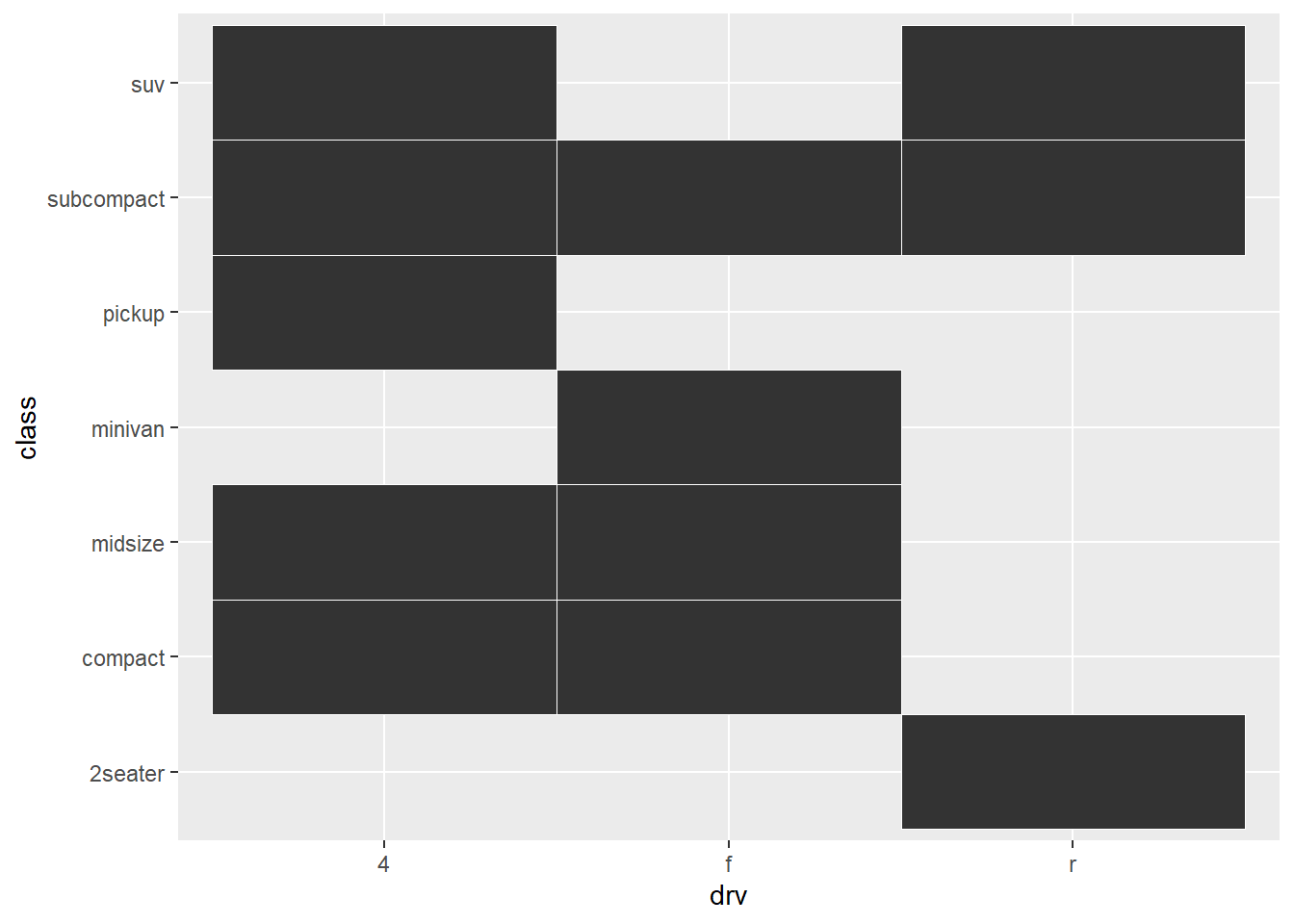
ggplot(mpg, aes(drv, class)) +
geom_bin2d(color = "white")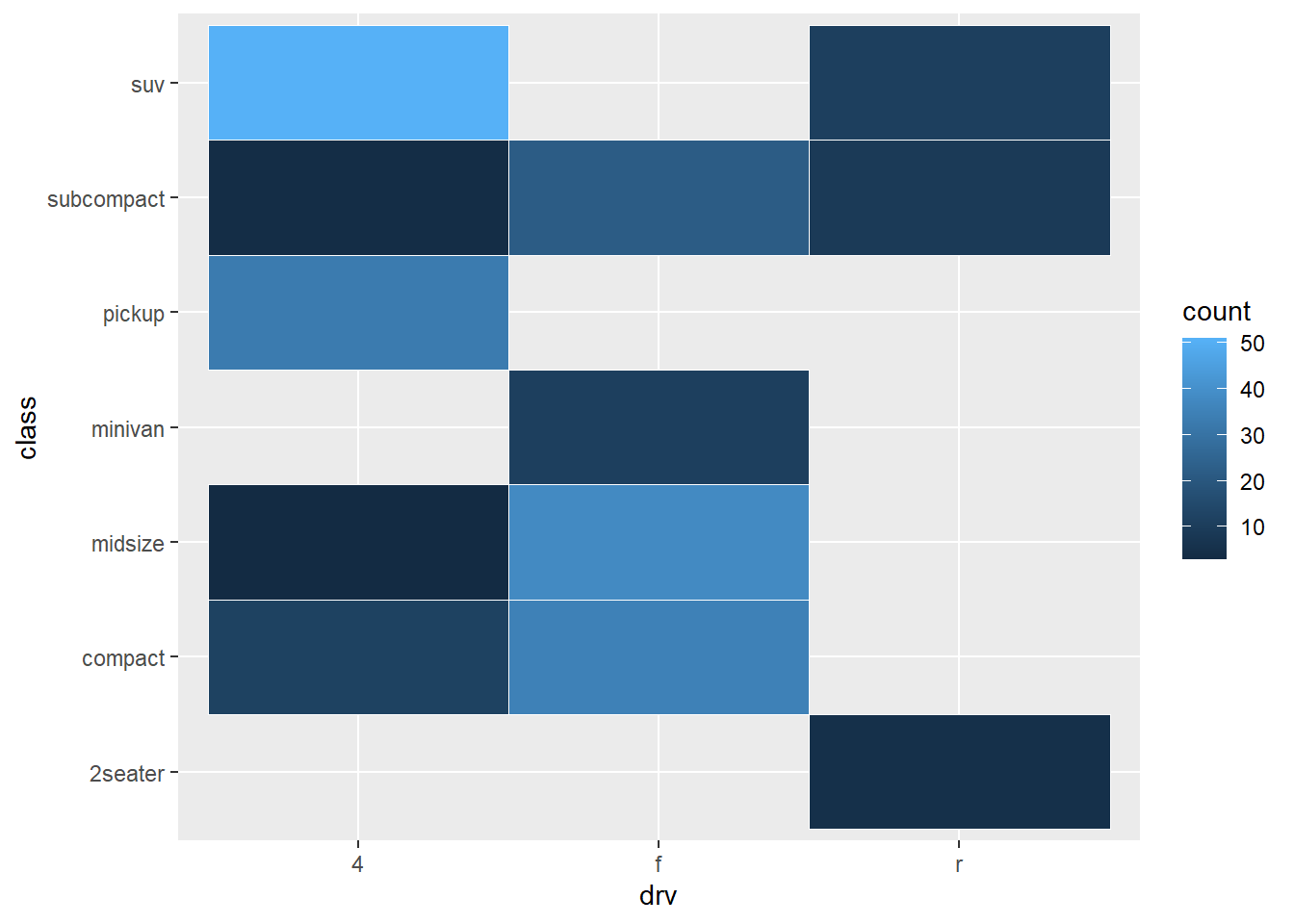
ggplot(mpg, aes(drv, class)) +
geom_hex(color = "white")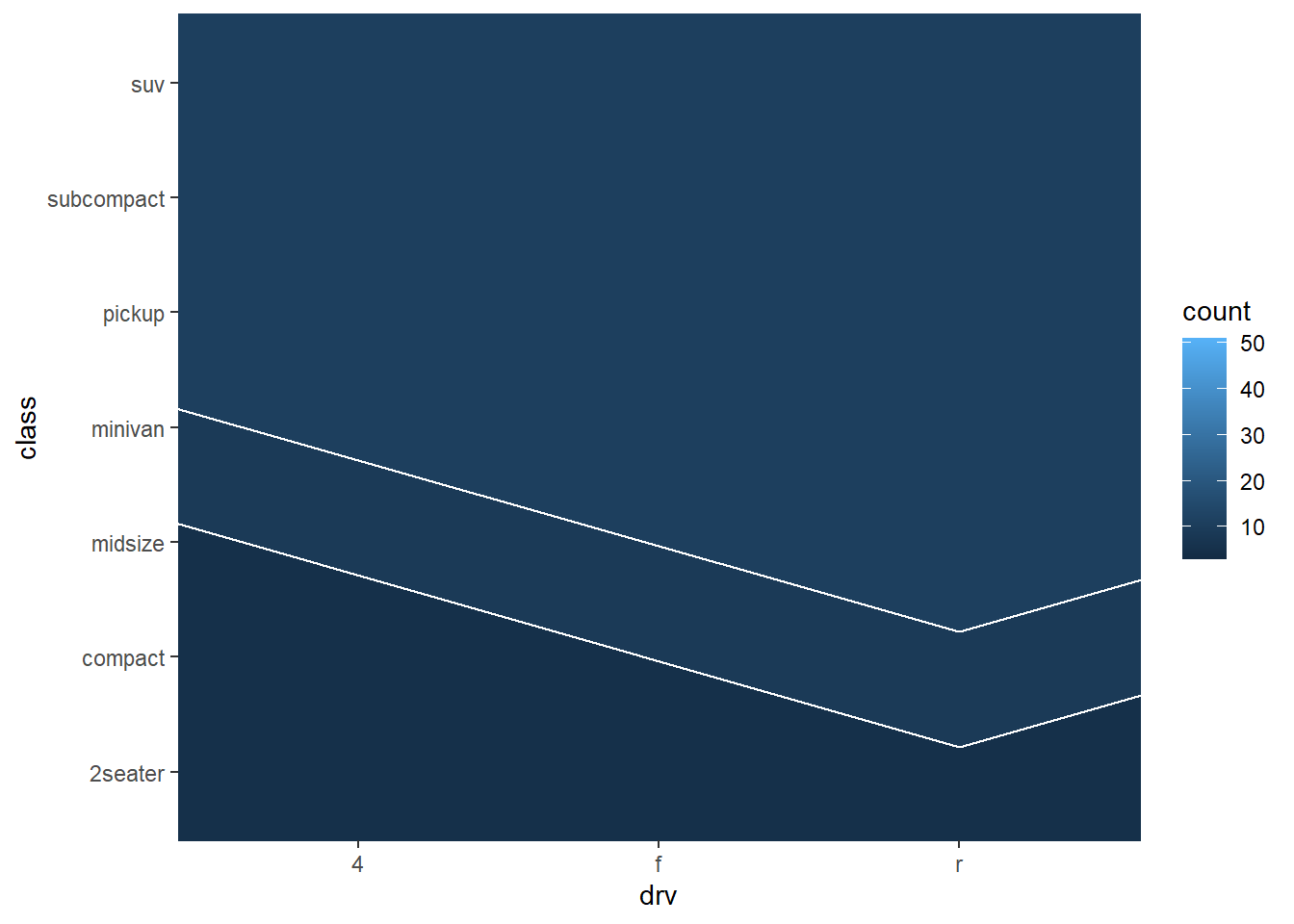
Volvamos al problema del overploting
Ya hemos mencionado que el overploting se da habitualmente cuando trabajamos con variables discretas (que generalmente generan menos posiciones que las cuantitativas) y el geom dibuja una marca por cada fila, ya que las marcas se van apilando perfectamente una sobre la otra, dando la sensación de que solo hay una.
Hemos usado position = "jitter" para “desenmascarar” el problema con geom_point(), pero ¿qué pasa con geom_bar(), geom_tile() o geom_bin2d()?
Si aplicamos jittering a un gráfico de barras, veremos que efectivamente las barras aparecen ligeramente desplazadas, pero tenemos una única barra/marca gráfica por cada nivel de la variable discreta:
ggplot(mpg, aes(class)) +
geom_bar(position = "jitter", color = "white")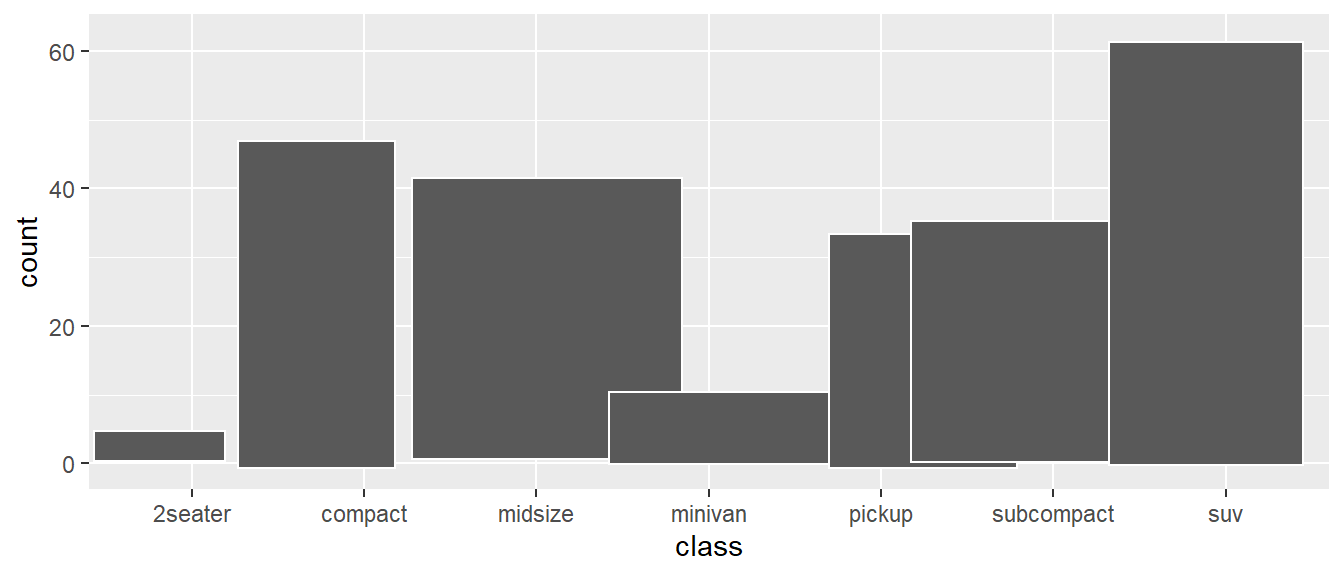
ggplot(mpg, aes(class)) +
stat_summary(aes(y = cty), fun = median, geom = "col", color = "white", position = "jitter")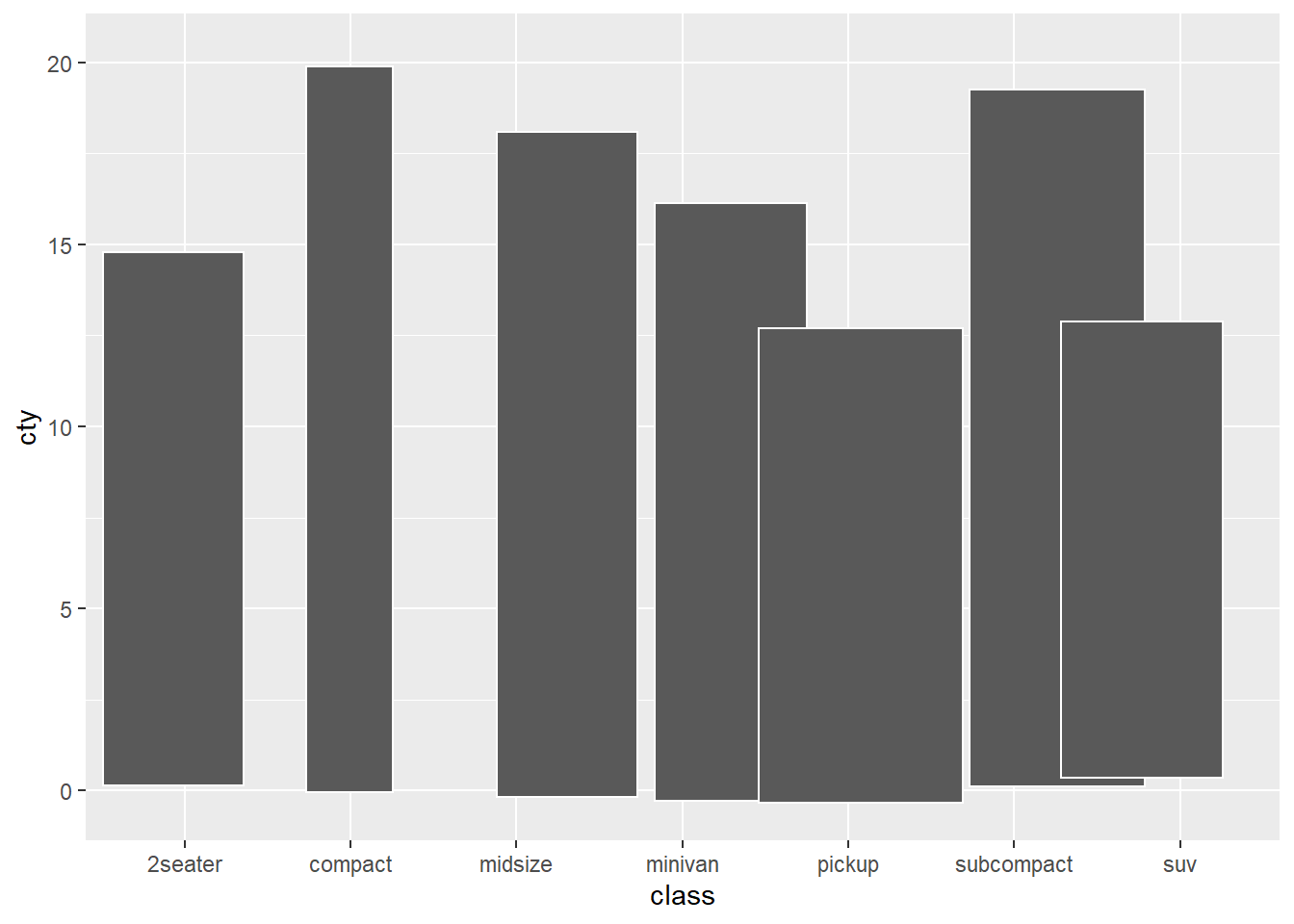
Si cruzamos dos variables discretas, se creará una marca por cada cruce con datos y, en el caso de geom_col se irán apilando una sobre la otra, ya que esa las configuración por defecto de position para ese geom..
ggplot(mpg, aes(class, cty)) +
geom_col(color = "white")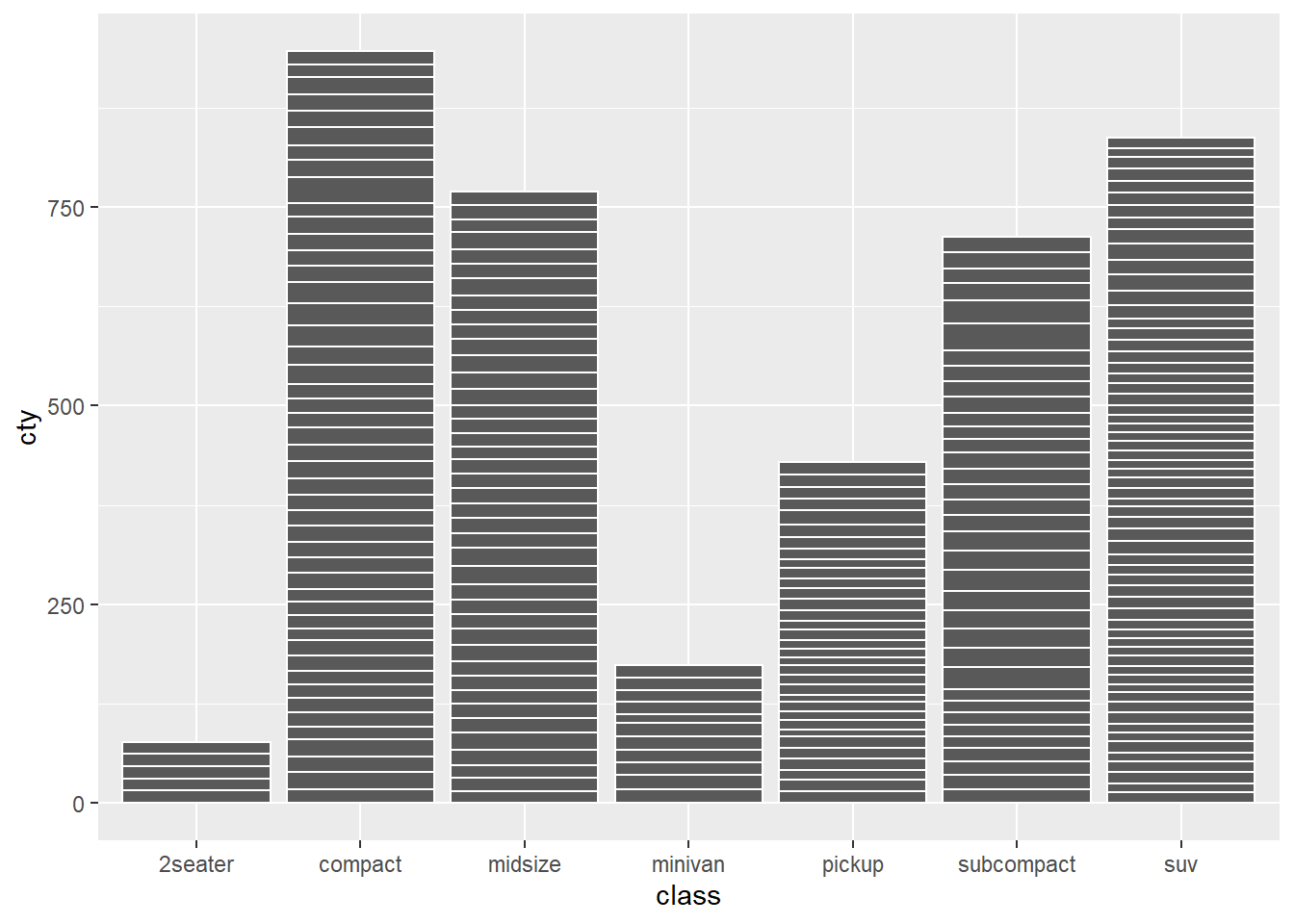
¿Y los geoms rectangulares?
ggplot(mpg, aes(drv, class)) +
geom_tile(color = "white")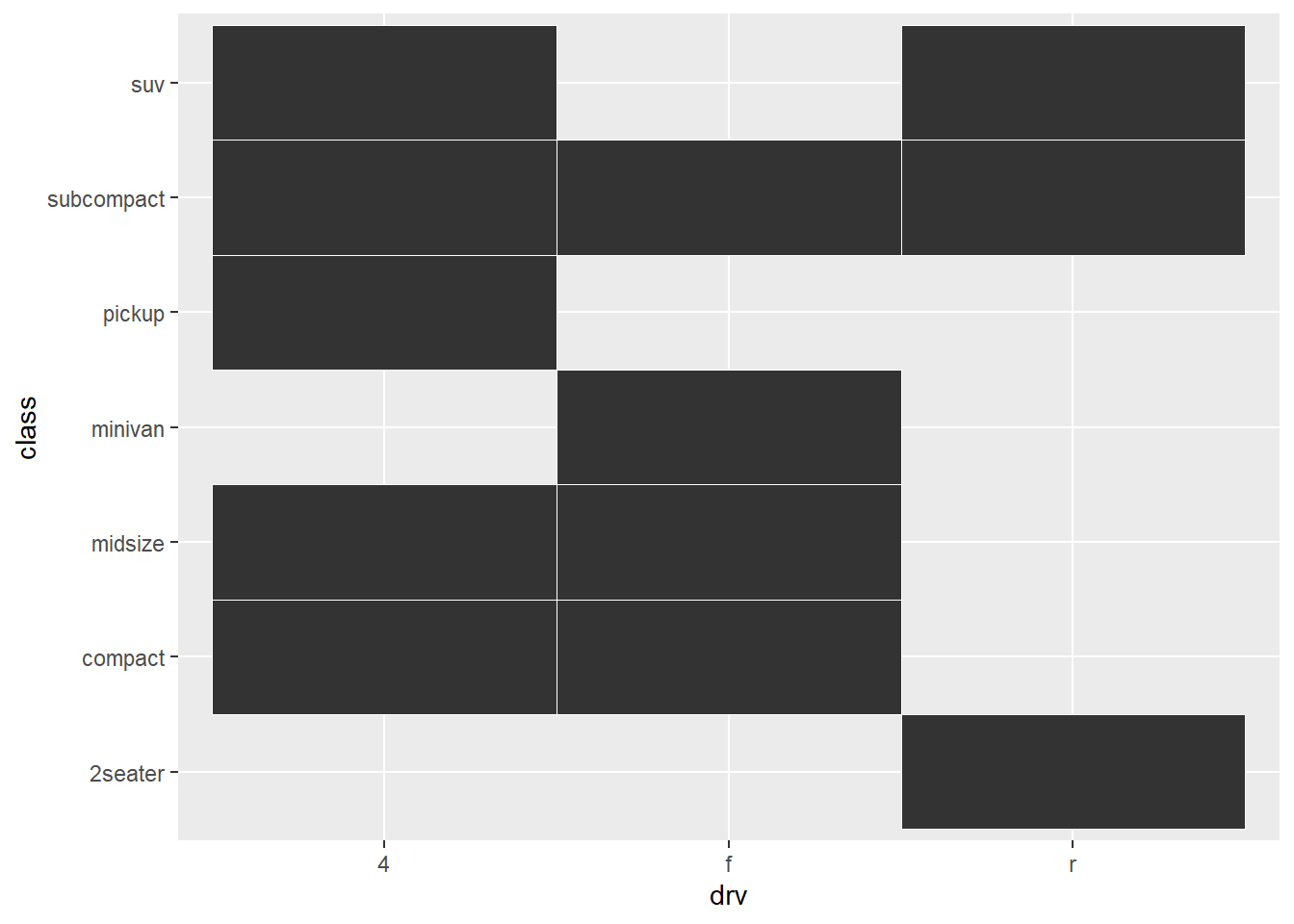
ggplot(mpg, aes(drv, class)) +
geom_bin2d(color = "white", position = "jitter")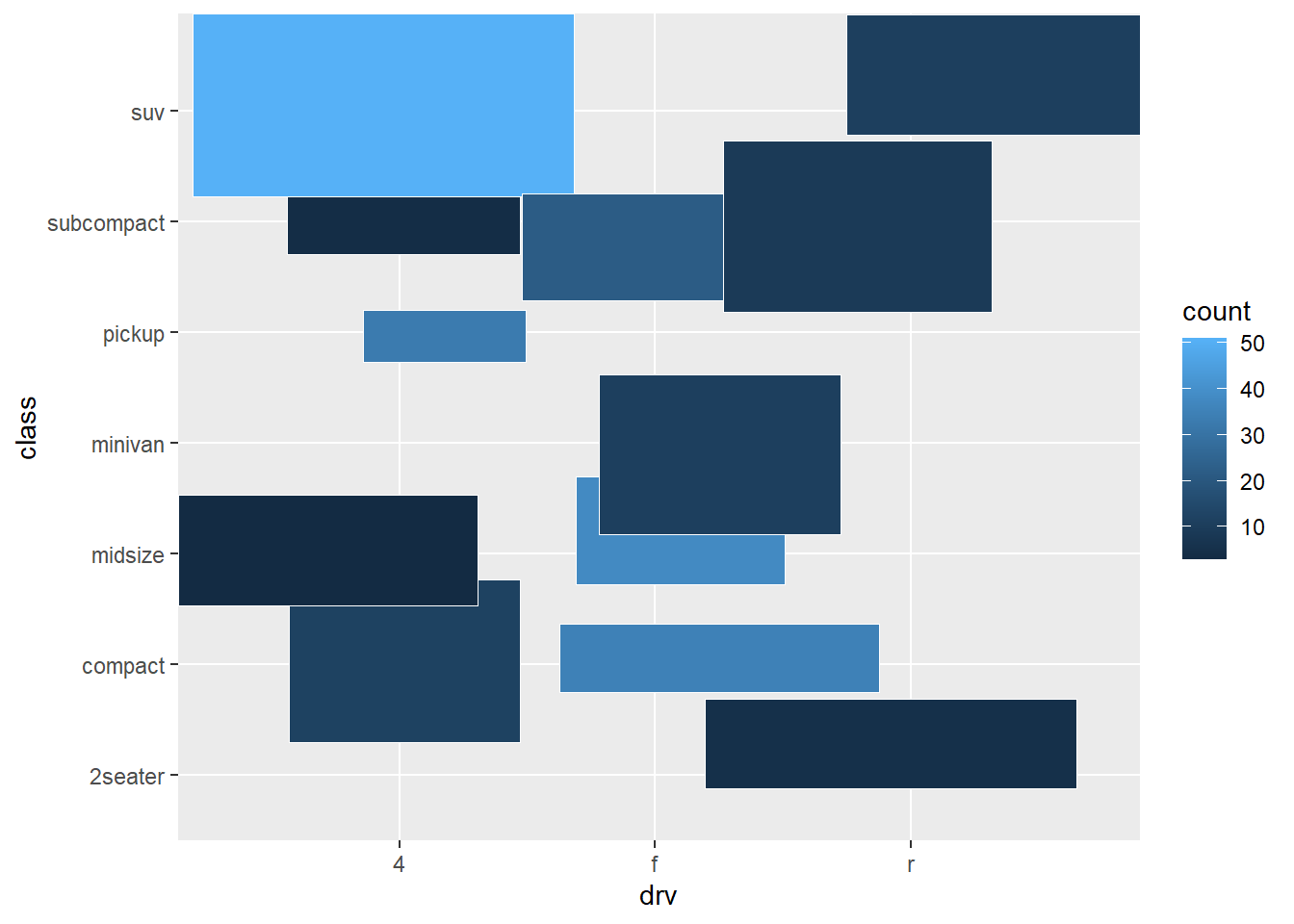
ggplot(mpg, aes(drv, class)) +
geom_tile(color = "white", position = "jitter")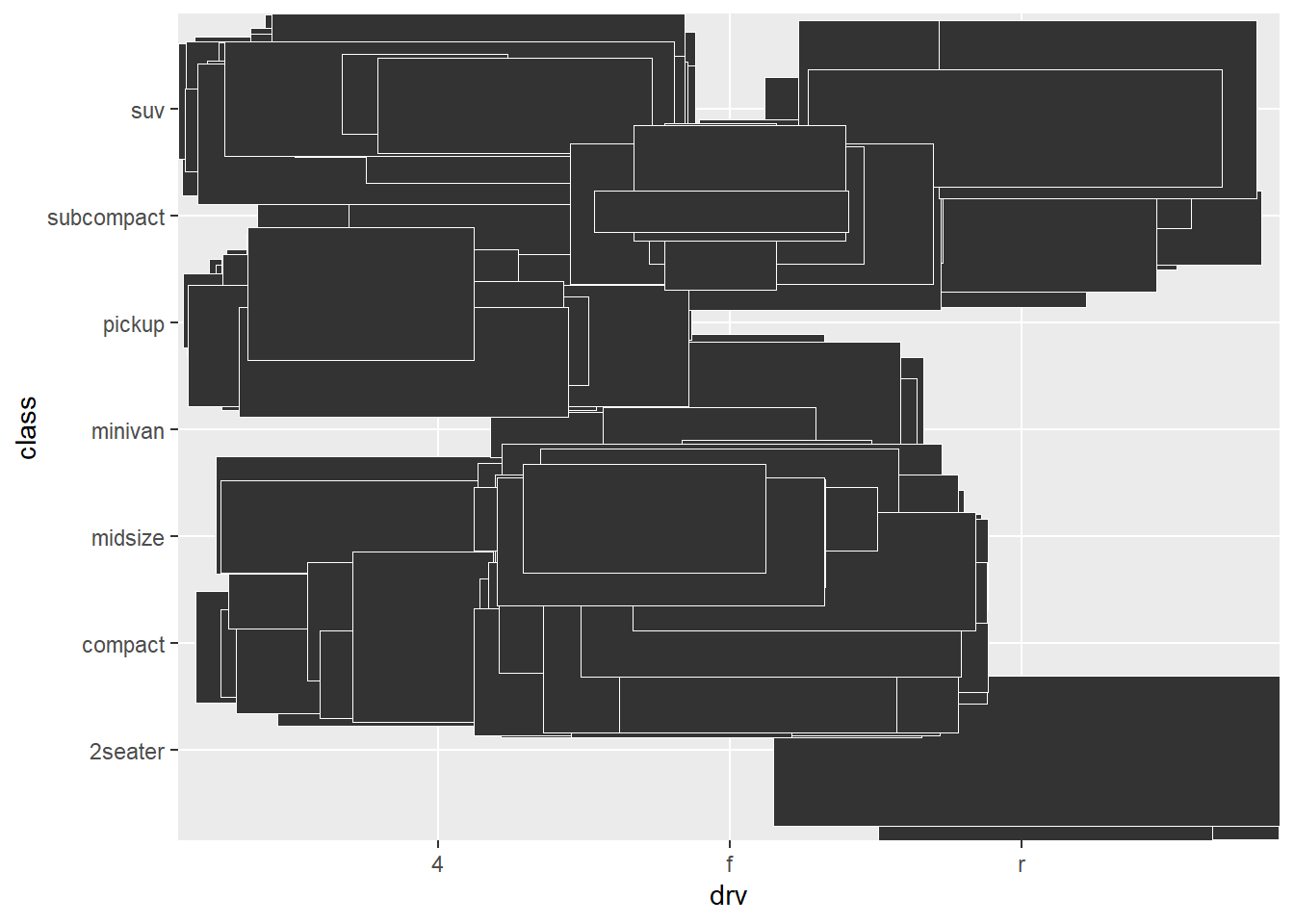
El comportamiento es el que ya hemos observado hasta ahora con otros geoms:
- Los
geomsque tienen unstatque cuenta (geom_bin2()) crean una única marca por cada localización; el número total de marcas viene dado por los argumentos de clasificación (bins,bindwidth). geom_tile()funciona comogeom_point(), creando una marca por cada fila del conjunto de datos, y si el punto dentral coincide, las va superponiendo.
Es importante que seamos conscientes de este funcionamiento de ggplot, ya que de otra forma podemos cometer errores de bulto a la hora de interpretar los gráficos que creamos, sobre todo si añadimos nuevas variables.
ggplot(mpg, aes(drv, class, fill = model)) +
geom_tile(color = "white")
Visto este gráfico, interpretaríamos, por ejemplo, que solo hay un modelo de tipo suv y 4, que sería el gti o el impreza awd (ahora mismo conocer el color exacto no es importante, ya que partimos de que el gráfico es incorrecto). Sin embargo esta interpretación es incorrecta, ya que gti o impreza awd es simplemente la última fila que tiene los valores suv y 4 para las variables que hemos mapeado en x e y.
La leyenda de color nos está dando una pista de que en el gráfico hay más de lo que vemos, porque muestra más niveles de color que marcas vemos.
Si aplicamos jittering lo vemos mejor:
ggplot(mpg, aes(drv, class, fill = model)) +
geom_tile(color = "white", position = "jitter")
Así que con un poco de dplyr y una paleta de color personalizada, podemos crear nuestro propio Mondrian con unas pocas líneas de código.
mondrian_colors <- c(
"d" = "#fff001",
"e" = "#ff0101",
"p" = "#0101fd",
"r" = "#f9f9f9",
"c" = "#30303a"
)
mondrian_data_1 <- mpg %>%
filter(fl %in% c("d","e"))
mondrian_data_2 <- mpg %>%
filter(fl == "p") %>%
top_n(5,cty)
mondrian_data_3 <- mpg %>%
filter(fl == "r") %>%
top_n(3, cty)
mondrian_data <- bind_rows(mondrian_data_1, mondrian_data_2, mondrian_data_3)
ggplot(mondrian_data, aes(drv, trans, fill = fl)) +
geom_tile(position = "jitter", color = "black") +
theme_void() +
scale_fill_manual(values = mondrian_colors) +
guides(fill = FALSE)